

14.9 非线性降维和局部多维缩放

原文	The Elements of Statistical Learning
翻译	szcf-weiya
发布	2016-09-30
更新	2020-02-20 15:46:34
状态	Done

最近有人提出了一些用于非线性降维的方法，类似主曲面的思想．想法是将数据看成位于一个嵌在高维空间中的 固有低维非线性流形 (intrinsically low-dimensional nonlinear manifold) 的附近．这些方法可以看成是“压扁(flattening)”流形，因此将数据降低至低维坐标系统中，用于表示点在流形中的相对位置．在信噪比非常高的问题中非常有用（比如，物理系统），而且对于有低信噪比的观测数据不是很有用．

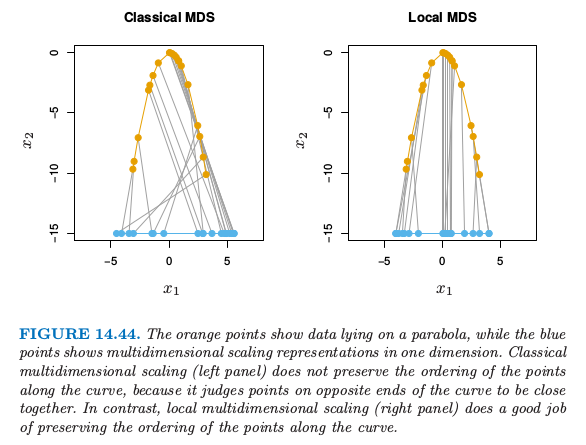
基本的目标在图 14.44 的左图中进行了说明．数据落在有较大曲率的抛物线附近．经典的 MDS 不能保持沿着这条曲线的点的顺序，因为它会将处于曲线两端的点看成离得非常近．右图显示了 局部多维缩放 (local multi-dimensional scaling, Local MDS) 的结果，我们将在下面讨论非线性多维缩放的三个方法中的其中一个．这些方法仅仅使用 $p$ 维中点的坐标，不需要流形的其它信息．局部多维缩放 能够很好地保持沿着曲线的点的顺序．

我们将简短地介绍用作非线性降维和流形映射的三个新方法．

等距特征映射算法 (Isometric feature mapping, ISOMAP) (Tenenbaum et al. 2000¹) 构造了一个图来近似沿着流形的点之间的测地线距离．具体地，对每个数据点，我们找到其邻居——距该点的某个欧式距离范围内的点．我们构造任意两个邻居点间用边相连的图．任意两点的测地线距离则用图中点的最短路径来近似．最终，对图的距离应用经典缩放，来得到低维映射．

局部线性内嵌 (Local linear embedding, LLE)(Roweis and Saul, 2000²)采用完全不同的方式，它试图保持高维数据的局部仿射结构．每个数据点用邻居点的线性组合来近似．于是通过寻找保持局部近似的最优方式构造低维表示．细节非常有趣，所以在这里给出：

1. 对每个 $p$ 维中的数据点 $x_i$，寻找欧式距离意义下的 $K$ 最近邻点 $\cal N(i)$.
2. 对每个点用邻居点的混合仿射来近似 $$\underset{w_{ik}}{\min}\Vert x_i-\sum\limits_{k\in\cal N(i)}w_{ik}x_k\Vert^2\tag{14.102}$$ 其中权重 $w_{ik}$ 满足 $w_{ik}=0, k\not\in \cal N(i), \sum_{k=1}^Nw_{ik}=1$．$w_{ik}$ 是点 $k$ 对 $i$ 点的重构的贡献．注意到为了得到唯一解，我们必须要求 $K < p$．
3. 最后，固定 $w_{ik}$，在 $d < p$ 维空间中寻找点 $y_i$ 来最小化 $$\sum\limits_{i=1}^N\Vert y_i-\sum\limits_{k=1}^Nw_{ik}y_k\Vert^2\tag{14.103}$$

在第三步，我们最小化

$$\tr [(\Y-\W\Y)^T(\Y-\W\Y)] = \tr[\Y^T(\I-\W)^T(\I-\W)\Y)]\tag{14.104}$$

其中 $\W$ 是 $N\times N$; $\Y$ 是 $N\times d, d < p$．$\hat \Y$ 的解是 $\M=(\I-\W)^T(\I-\W)$ 的 尾特征向量 (trailing eigenvectors)．因为 $\1$ 是特征值为 0 的平凡特征向量，所以我们舍弃它并且保留接下来的 $d$ 个．这会产生额外的影响 $\1^T\Y=0$，因此嵌入坐标的均值为0．

weiya 注:

这里的尾特征向量除去了特征值为 0 的平凡特征向量 $\1$，而因为特征向量间正交，所以有 $\1^T\Y=0$.

局部多维缩放 (Local MDS)（Chen and Buja, 2008³）采用最简单的、而且可以说是最直接的方式．定义 $\cal N$ 为邻居点的对称集；具体地，如果点 $i$ 在 $i’$ 的 $K$ 最近邻中，则点对 $(i, i’)$ 在 $\cal N$ 中，反过来也是如此．

weiya 注

在14.7节中的谱聚类的 mutual K-nearest-neighbor graph 也有用到 $\cal N$．

于是我们构造压力函数

$$S_L(z_1,z_2,\ldots, z_N) = \sum\limits_{(i,i')\in \cal N}(d_{ii'}-\Vert z_i-z_{i'}\Vert)^2 + \sum\limits_{(i,i')\not\in \cal N}w\cdot (D-\Vert z_i-z_{i'}\Vert)^2\tag{14.105}\label{14.105}$$

这里 $D$ 是某个较大的常数，$w$ 是权重．想法是将不是邻居的点看成是距离非常远；这些点对被赋予小权重 $w$ 使得它们不会主导整个压力函数．为了简化表达式，取 $w\sim 1/D$，并令 $D\rightarrow \infty$．展开式 \eqref{14.105}，得到

$$S_L(z_1,z_2,\ldots, z_N)=\sum\limits_{(i, i')\in\cal N}(d_{ii'}-\Vert z_i-z_{i'}\Vert)^2-\tau \sum\limits_{(i,i')\not \in \cal N}\Vert z_i-z_{i'}\Vert\tag{14.106}\label{14.106}$$

其中 $\tau =2wD$．式 \eqref{14.106} 试图保持数据的局部性质，而第二项促使非邻居对 $(i, i’)$ 的 $z_i,z_{i’}$ 更远．局部多维缩放在固定邻居个数 $K$ 以及调整参数 $\tau$ 的情况下，在 $z_i$ 上最小化压力函数 \eqref{14.106}．

图 14.44 的右图显示了采用 $k=2$ 个邻居和 $\tau = 0.01$ 的局部多维缩放的结果．我们采用多个起始值的 坐标下降 (coordinate descent) 来寻找（非凸）损失函数一个好的最小值．沿着曲线的点的顺序大部分都被保持了．

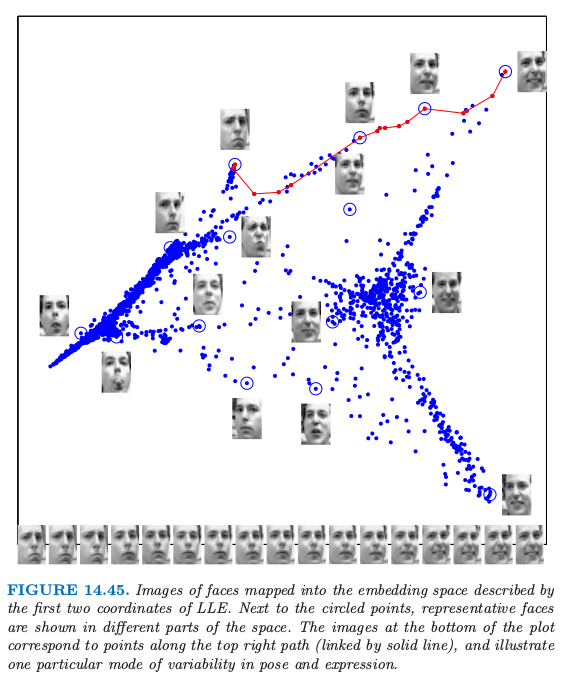
图 14.45 显示了 LLE 方法的一个有趣的应用．数据包含 1965 张图象，数字化为 $20\times 28$ 的灰白图象．图中展示了 LLE 的前两个坐标结果，它们解释了摆放位置以及表情的一些变异．类似的图象可以通过局部多维缩放得到．

原书脚注:

Sam Roweis 和 Lawrence Saul 友好地提供了图 14.45.

在 Chen and Buja(2008)³ 报告的实验中，局部多维缩放与 ISOMAP 和 LLE 相比表现得更好．他们也演示了局部多维缩放在图象布局方面很有用的应用．有些方法与这里讨论的方法有着紧密的联系，如谱聚类（14.5.3 节）和核主成分（14.5.4 节）．

---

1. Tenenbaum, J. B., de Silva, V. and Langford, J. C. (2000). A global geometric framework for nonlinear dimensionality reduction, Science 290: 2319–2323. ↩

2. Roweis, S. T. and Saul, L. K. (2000). Locally linear embedding, Science 290: 2323–2326. ↩

3. Chen, L. and Buja, A. (2008). Local multidimensional scaling for nonlinear dimension reduction, graph drawing and proximity analysis, Journal of the American Statistical Association. ↩↩

Comments