模拟:Fig. 5.9¶
| 原文 | 5.5 光滑参数的自动选择 |
|---|---|
| 作者 | szcf-weiya |
| 发布 | 2018-03-30 |
生成数据¶
模型为
其中 $X\sim U[0,1], \varepsilon\sim N(0, 1)$。
## generate dataset
func <- function(x)
{
return(sin(12*(x+0.2))/(x+0.2))
}
genXY <- function(N = 100)
{
x = runif(N)
noise = rnorm(N)
y = func(x) + noise
return(list(X = x,
Y = y))
}
计算 CV¶
错误的做法¶
在 R 中,可以用smooth.spline() 来拟合三次光滑样条。一开始,注意到该函数返回值有 LOOCV (或 GCV),于是觉得只用一个循环就可以得到交叉验证随自由度变化的曲线(原图中的交叉验证便是舍一法),即
nrep = 15
df.seq = (1:nrep)+1
models = vector("list", nrep)
cvs = numeric(nrep)
for (i in 1:nrep){
models[[i]] = smooth.spline(X, Y, df = df.seq[i], cv=TRUE, all.knots = TRUE)
cvs[i] = models[[i]]$cv.crit
}
但这样得到的图象为
这与图 5.9 的图象完全不一样,曲线走势还是相反的,所以这样理解是有问题的。详细阅读帮助文档,我的结论是,虽然我们指定了有效自由度 $\df_\lambda$,但模型参数中的交叉验证还是用来进行模型选择,因为还有一个参数 spar 可以调整样条的光滑度,这一点书上似乎没有提到。所以便根据定义自己编写适用的计算 CV 的函数
自定义函数¶
直接根据舍一法交叉验证公式进行计算
mysmooth.spline <- function(X, Y, df){
nY = length(Y)
nX = length(X)
cv.i = as.numeric(nX)
if (nX != nY)
return(0)
# calculate LOOCV
for (i in 1:nX){
x = X[-i]
y = Y[-i]
model = smooth.spline(x, y, df = df, all.knots = TRUE)
cv.i[i] = (Y[i] - predict(model, X[i])$y)^2
}
cv = mean(cv.i)
# calculate EPE
# ...
}
计算 CV¶
定义式为
问题是怎么求期望呢?
第一次尝试¶
第一次尝试是与上述计算 CV 时的错误做法一起发生的,因为注意到函数有个返回值 pens.crit,帮助文档给出的解释为
the penalized criterion, a non-negative number; simply the (weighted) residual sum of squares (RSS), sum(.$w * residuals(.)^2)
于是用
crits[i] = models[[i]]$crit
来估计 EPE,但发现这样还是与原图有很多差异,非常重要的一点是这个准则是随着 $\lambda$ 变大而单调降低的。
第二次尝试¶
观察 (5.25) 的最后一行,认为 $\sigma^2=\sigma_\varepsilon^2=1$,然后估计 MSE ,最后效果也不好
Y.pred = model.full$y
Y.true = func(model.full$yin) # DO NOT use Y directly, because they have reordered.
epe = 1 + mean(( Y.true - Y.pred)^2)
效果也和原书有差异,遂放弃。
第三次尝试¶
这时,意识到计算 EPE 时应该不能在测试集上计算,所以这次尝试和下面的尝试都是在测试集上进行。这一次,测试时重新生成测试集,然后计算 EPE(直接用定义式来估计),即
data.test = genXY(N = 500)
x.test = data.test$X
y.test = data.test$Y
y.pred = predict(model.full, x.test)$y
epe = mean((y.test - y.pred)^2)
此时的效果已经非常接近图 5.9 了,但突然意识到一个问题,我们应该是不知道真实数据的生成过程,不然还需要拟合么?所以测试集还是只来自仅有的 $N=100$ 个观测值。
第四次尝试¶
这一次,将 $N=100$ 划分为测试集和训练集,在测试集上计算 EPE,即
n2 = 100
epe.i = numeric(n2)
for (i in 1:n2){
ind = sample(N, 50)
model = smooth.spline(X[ind], Y[ind], df = df)
y.pred = predict(model, X[-ind])$y
epe.i[i] = mean((y.pred - Y[-ind])^2)
}
epe = mean(epe.i)
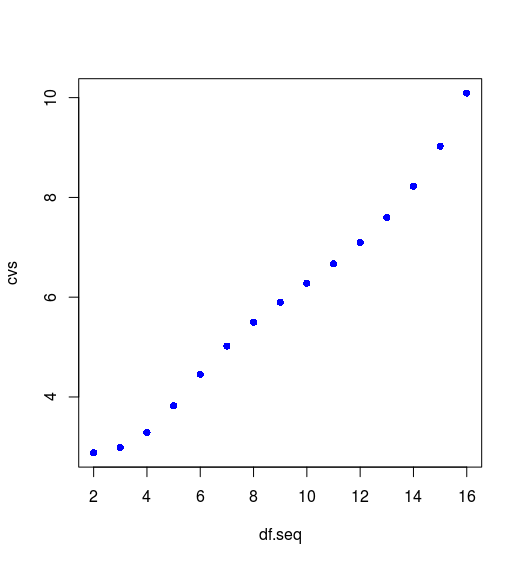
此时的效果已经非常接近原图了,如下图

虽然个别误差比原图稍大,但趋势与原图完全一致,最小值也在 $9$ 附近取得。
给定 $\lambda$¶
现在已经重现了左上图,对于剩下三幅图,我们需要计算平均的拟合值以及方差,这可以直接在上述求 EPE 的过程(或者求 CV 时)中计算,
yhat = array(dim = c(n2, nY))
epe.i = numeric(n2)
for (i in 1:n2){
# ...
# predict the whole dataset
yhat[i, ] = predict(model, sort(X))$y
}
## calculate the mean and sd of fitted value
yhat.mean = apply(yhat, 2, mean)
yhat.sd = apply(yhat, 2, sd)
然后在编写下面的绘图函数
## plot function for (b)-(d)
plot.lambda <- function(X, Y, lambda)
{
res = mysmooth.spline(X, Y, lambda)
fitted = res$fitted
sd = res$sd
plot(X, Y, xlab = expression(X), ylab = "y",
main = substitute(paste(df[lambda]," = ", l), list(l=lambda)))
lines(0.01*0:100, func(0.01*0:100), col = "blue", type = "l", lwd=3)
lines(sort(X), fitted, lwd = 3)
polygon(c(rev(sort(X)), sort(X)), c(rev(fitted-2*sd), fitted+2*sd),
col=rgb(1, 1, 0, 0.5), border = NA)
}
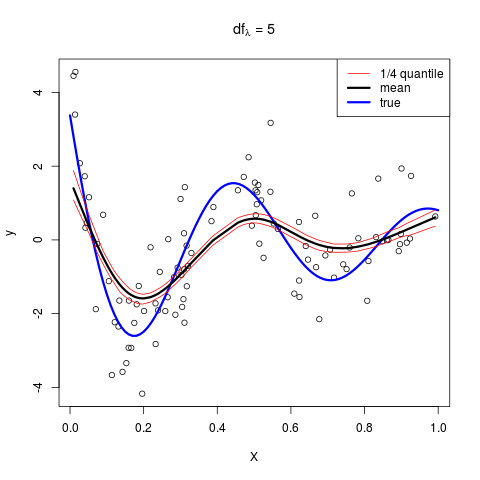
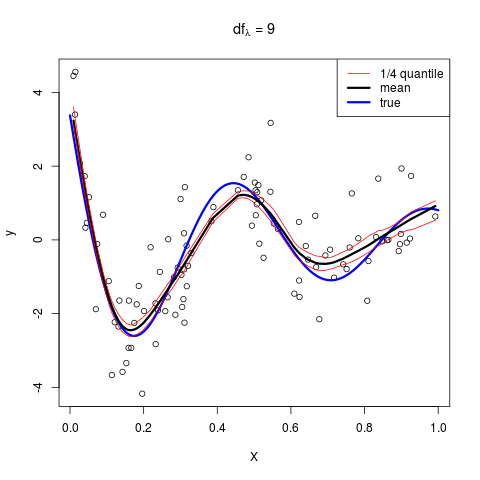
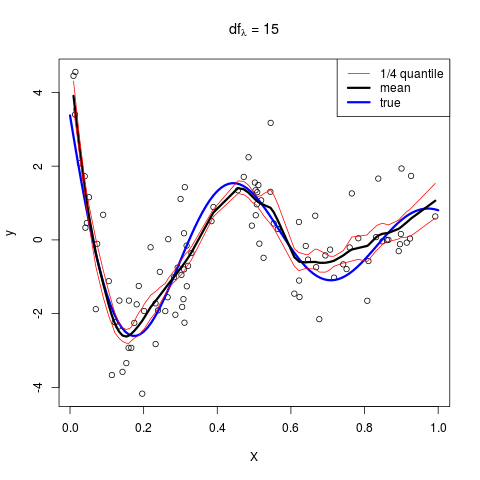
则依次取 $\lambda=5,9,15$,可以得到
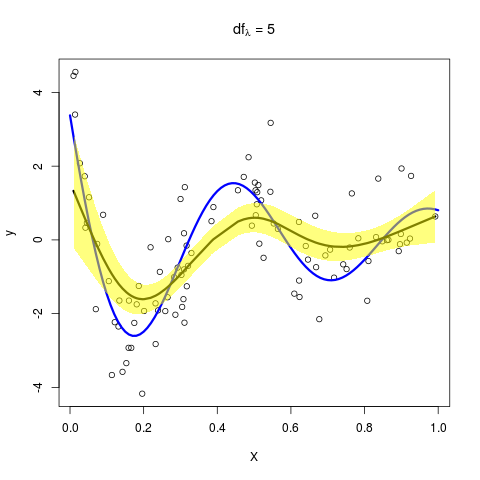
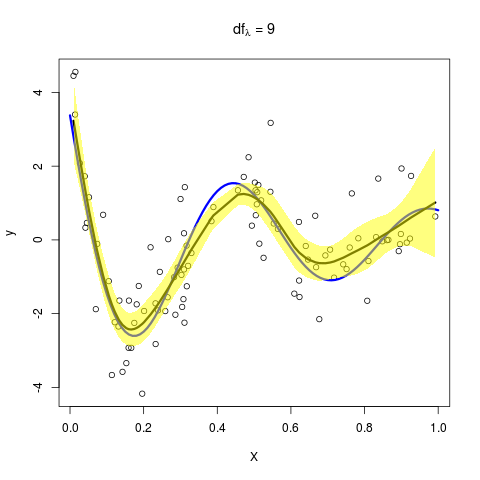
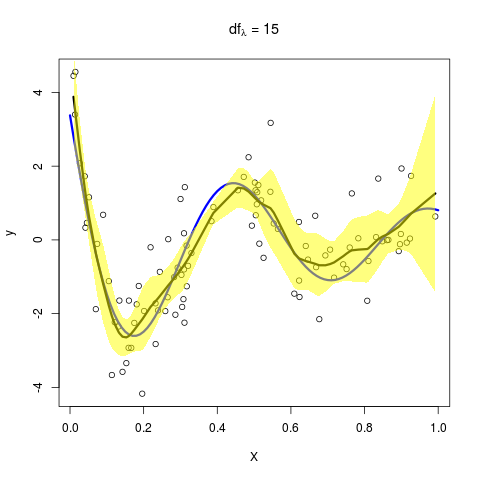
这与原图是一致的!
练习 5.10¶
Ex. 5.10 要求添加 $\hat f(\lambda)$ 的逐点分位数,直接在上面的代码中加入计算分位数的代码即可
yhat75 = apply(yhat, 2, function(x) quantile(x, 0.75))
yhat25 = apply(yhat, 2, function(x) quantile(x, 0.25))
得到