10.8 例子: 垃圾邮件¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2017-06-09 |
| 更新 | 2020-01-14 14:53:37 |
| 状态 | Done |
在我们讨论 gradient boosting 的细节之前,首先用一个二分类的问题来说明它的能力.垃圾邮件数据在第一章以及有过介绍,并且第 9 章的很多方法都将其作为例子(第 9.1.2,9.2.5,9.3.1,以及 9.4.1).
对和 9.1.2 节一样的测试集应用 gradient boosting 会得到 4.5% 的测试误差.比较来看,可加逻辑斯蒂回归达到 5.5%,全生长并通过交叉验证剪枝 (fully grown and pruned by cross-validation) 的 CRAT 达到 8.7%,而 MARS 5.5%. 这些估计的标准差大概在 0.6%,通过 McNemar 检验,gradient boosting 显著地要比其它的好(练习 10.6).
weiya 注:Ex. 10.6
已解决,详见 Issue 214: Ex. 10.6.
在后面的 10.13 节,我们对每个预测变量构造出相对重要性度量,以及描述变量对拟合模型的贡献的 偏相依图 (partial dependence plot).我们现在对垃圾邮件数据说明这一点.
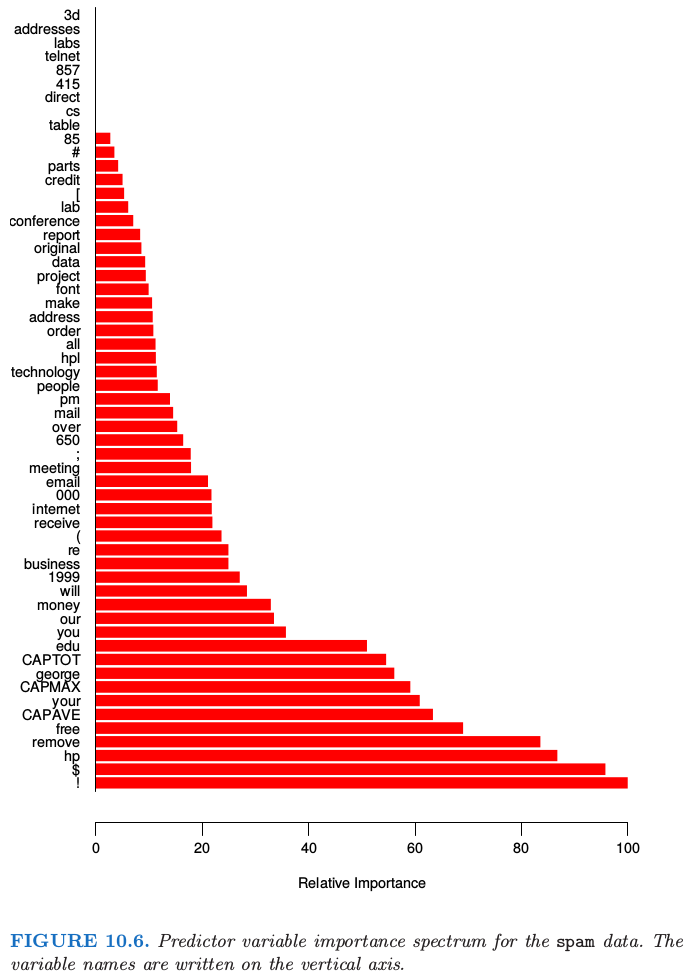
图 10.6 展示了对所有 57 个预测变量的相关重要性谱图.很明显,有些变量在将 spam 从 email 分离方面会更重要.字符串 !, $, hp 以及 remove 是四个最相关的预测变量.而在频谱的末端,字符串 857, 415, table 和 3d 差不多没什么关系.
这里建模的是 spam 相对于 email 的对数比率,
(见后面的 10.13 节).
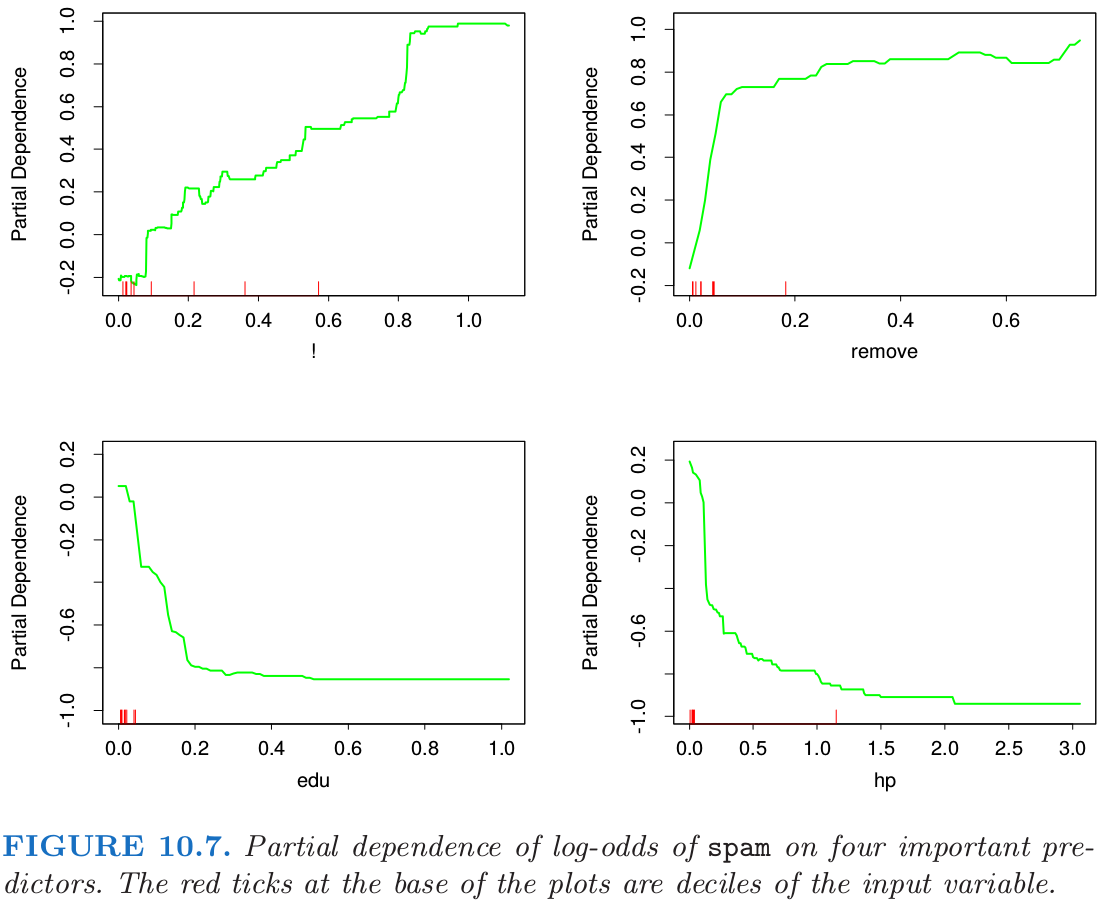
图 10.7 展示了对数比率在已选的重要预测变量上的偏相依性,! 和 remove 这两个跟 spam 正相关,以及两个负相关,edu 和 hp.这些特定的依赖性似乎本质上是单调的.这与通过可加逻辑斯蒂回归模型找到的对应的函数大体一致.见图 9.1.
weiya 注:图 9.1
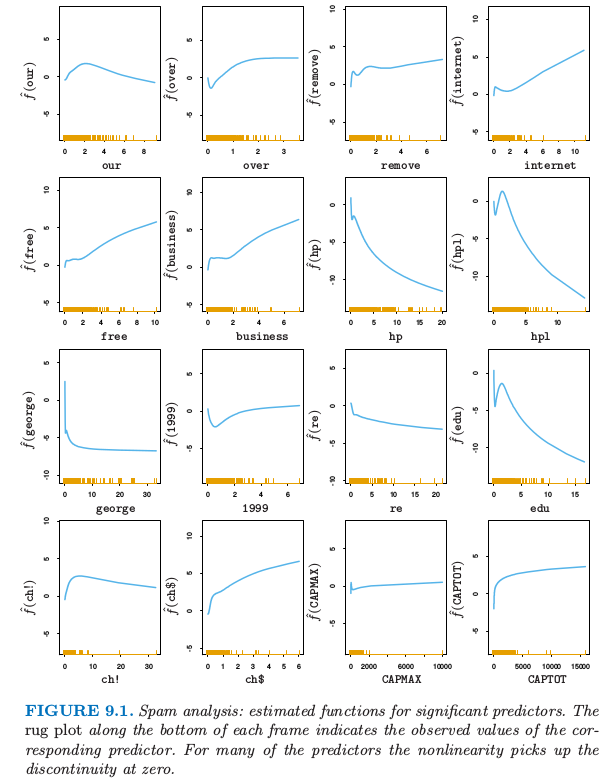
图 9.1 展示了关于 16 个预测变量的拟合函数,有三个共同预测变量,remove, edu 和 hp.从趋势上看,图 9.1 中这三个变量的拟合函数确实跟图 10.7 中对应的曲线趋势相同.
在这些数据上运行 $J=2$ 个终止结点的 gradient boosted 模型得到一个关于对数比率的完全可加模型(主要影响 (main effects)),对应的误差率为 4.7%,跟全 gradient boosted 模型(终止结点个数为 $J=5$)的 4.5% 相比.尽管不是显著差异,但是这略高的误差率表明在某些重要的预测变量间存在 交叉影响 (interactions).这可以通过双变量偏相依性图来诊断.图 10.8 展示了其中一张表现出强交叉影响的图.
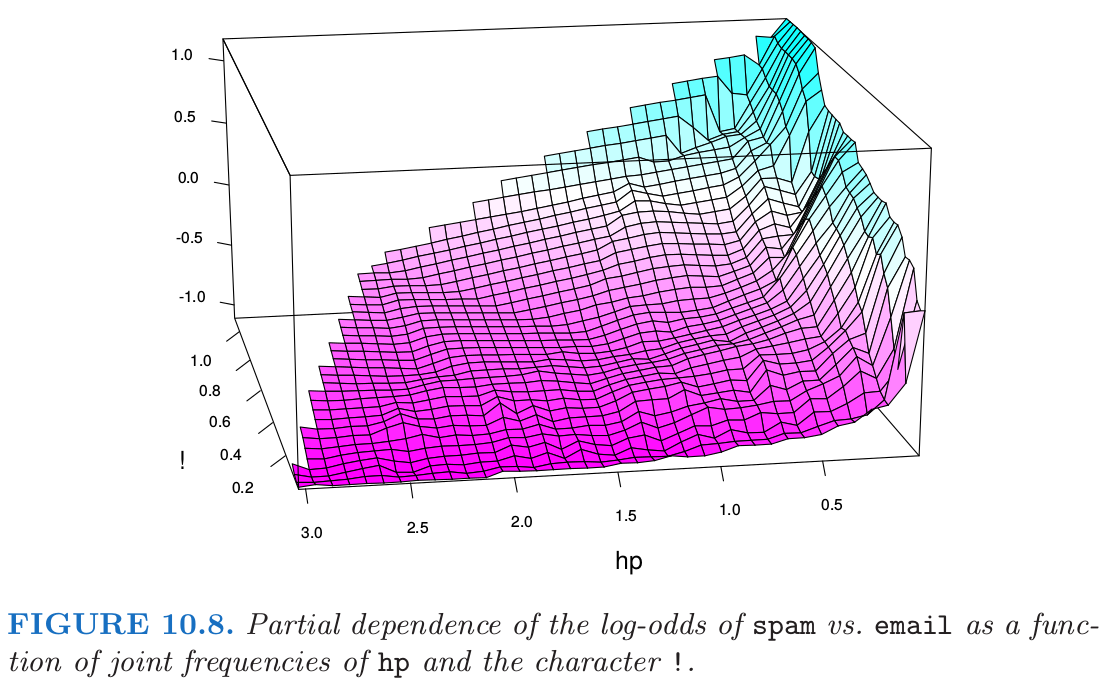
可以看到,对于频率非常低的 hp,spam 的对数比率大幅提高.对于高频率时的 hp,spam 的对数比率趋向于非常低,而且近似是 ! 的常数函数.当 hp 的频率降低时,其跟 ! 的函数关系在增强.