

5.8 正则化和再生核希尔伯特空间理论¶

原文	The Elements of Statistical Learning
翻译	szcf-weiya
发布	2017-06-09
更新	2020-02-26 22:52:43
状态	Done

这一节我们将样条放进更大的正规方法框架下以及 再生核希尔伯特空间 (reproducing kernel Hilbert spaces) 中．这部分非常专业 (quite technical)，因此不感兴趣或者有些畏惧的读者可以跳过．

一般的正则化问题形式如下

$\underset{f\in{\cal H}}{\min}\Big[ \sum\limits_{i=1}^NL(y_i,f(x_i))+\lambda J(f) \Big]\,, \tag{5.42}\label{5.42}$

其中 $L(y,f(x))$ 是损失函数，$J(f)$ 是惩罚函数，$\cal H$ 是 $J(f)$ 有定义的函数空间．Girosi et al. (1995)¹ 描述了形如下式的非常一般的惩罚函数

$J(f)=\int_{\IR^d}\frac{\vert \tilde f(s)\vert^2}{\tilde G(s)}ds \tag{5.43}\label{5.43}$

其中 $\tilde f$ 记为 $f$ 的 Fourier 变换，并且 $\tilde G$ 是当 $\Vert s\Vert\rightarrow \infty$ 趋于 $0$ 的正函数．上式想法是 $1/\tilde G$ 加大对 $f$ 的高频组分的惩罚．在一些额外的假设下，他们证明解有如下形式

$f(X)=\sum\limits_{k=1}^K\alpha_k\phi_k(X)+\sum\limits_{i=1}^N\theta_iG(X-x_i)\tag{5.44}$

其中 $\phi_k$ 张成惩罚函数 $J$ 的零空间，并且 $G$ 是 $\tilde G$ 的逆 Fourier 变换．光滑样条和 thin-plate 样条都属于这个框架．这个解的显著特点是当准则 \eqref{5.42} 定义在无限维空间，解是有限维．在下一节我们考虑一些具体的例子．

核产生的函数空间¶

形如 \eqref{5.42} 的问题的一个重要子类是由正定核 $K(x,y)$ 产生的，对应的函数空间 ${\cal H}_K$ 被称为 再生核希尔伯特空间 (reproducing kernel Hilbert space)，简称为 RKHS．惩罚函数也是用核来定义的．我们对这个模型类进行一个简短的介绍，这取自 Wahba (1990)² 和 Girosi et al. (1995)¹，并且在 Evgeniou et al. (2000)³ 中有很好的总结．

令 $x,y\in \IR^p$．我们考虑由 $\{K(\cdot, y), y\in \IR^p\}$ 线性张成的函数空间；也就是，形如 $f(x)=\sum_m\alpha_mK(x, y_m)$ 的任意线性组合，其中每个核可以看成第一个变量的函数，并且由第二个变量索引．假设 $K$ 有 特征展开 (eigen-expansion)

$K(x, y)=\sum\limits_{i=1}^\infty \gamma_i \phi_i(x)\phi_i(y)\tag{5.45}\label{5.45}$

其中 $\gamma_i\ge 0,\sum_{i=1}^\infty \gamma_i^2 < \infty$．

weiya 注：Mercer’s theorem

\eqref{5.45} 的分解由 Mercer’s theorem 保证，Mercer’s theorem 将半正定矩阵的特征分解推广到半正定核函数的特征分解，具体地，图片来源: Wiki: Mercer’s theorem．

${\cal H}_K$ 的元素是关于这些 特征函数 (eigen-functions) 的展开，即

$f(x)=\sum\limits_{i=1}^\infty c_i\phi_i(x)\tag{5.46}$

并且约束条件为

$\Vert f \Vert_{{\cal H}_K}^2\overset{def}{=}\sum\limits_{i=1}^\infty c_i^2/\gamma_i < \infty\tag{5.47}$

其中 $\Vert f\Vert_{{\cal H}_K}$ 由 $K$ 导出的范数．

weiya 注：Induced Norm

希尔伯特空间是完备内积空间，对于一般的希尔伯特空间 $\cal H$，其 导出范数 (induced norm) 为 $\Vert f\Vert_{{\cal H}} := \sqrt{\langle f,f\rangle_{{\cal H}}}\,.$

weiya 注：两种构造 RKHS 的方法

一般地，有两种构造 RKHS 的方法：

第一种，给定一个半正定核 $K$，定义映射 $\Phi:\calX\mapsto \IR^\calX$ 为 $\Phi(x) = K(\cdot, x)$，然后考虑向量空间 $\span(\{\Phi(x):x\in\calX\}) = \left\{f(\cdot) = \sum_{i=1}^N\alpha_iK(\cdot, x_i)\right\}\,,$ 并对 $f = \sum_{i=1}^N\alpha_iK(\cdot, u_i), g = \sum_{i=1}^N\beta_iK(\cdot, v_i)$ 定义内积 $\langle f, g\rangle = \sum_{i=1}^N\sum_{j=1}^N\alpha_i\beta_jK(u_i,v_j)\,,$ 则 $K$ 满足核再生性质，并且 $\overline{\span({\Phi(x)})}$ 定义了 RKHS.

另外一种，则是用 Mercer 定理，定义内积 $\langle f, g\rangle_{\calH} = \sum_{j=1}^{\infty}\frac{\langle f,\phi_j\rangle\langle g,\phi_j\rangle}{\mu_j}$ 则 $\left\{f=\sum_{j=1}^\infty c_j\phi_j\mid \sum_{j=1}^\infty c_j^2/\mu_j < \infty\right\}$ 为 RKHS.

参考 Wainwright (2019) 和 Peter Bartlett’s notes.

\eqref{5.42} 中空间 ${\cal H}_K$ 的惩罚函数定义为二次范数 $J(f)=\Vert f\Vert_{{\cal H}_K}^2$．$J(f)$ 的值可以解释为广义岭惩罚，其中在展开式 \eqref{5.45} 中，大的特征值惩罚较小，反之亦然．

重写 \eqref{5.42}，我们有

$\underset{f\in {\cal H}_K}{\min}\Big[\sum\limits_{i=1}^NL(y_i, f(x_i))+\lambda \Vert f\Vert_{{\cal H}_K}^2\Big]\tag{5.48}\label{5.48}$

或者等价地，

$\underset{\{c_j\}_1^\infty}{\min}\Big[\sum\limits_{i=1}^NL(y_i, \sum\limits_{j=1}^\infty c_j\phi_j(x_i))+\lambda \sum\limits_{j=1}^\infty c_j^2/\gamma_j\Big]\tag{5.49}\label{5.49}$

可以证明（Wahba, 1990², 另见练习 5.15），\eqref{5.48} 的解是有限的，并且如下形式

$f(x)=\sum\limits_{i=1}^N\alpha_i K(x, x_i)\tag{5.50}\label{5.50}$

weiya 注：Ex. 5.15

已解决，详见 Issue 163: Ex. 5.15, 其中证明了再生核性质。

基函数 $h_i(x)=K(x,x_i)$（关于第一个变量的函数）被称作 ${\cal H}_K$ 中 $x_i$ 处的 representer of evaluation，因为对于 $f\in {\cal H}_K$，容易看到 $\langle K(\cdot, x_i),f\rangle_{{\cal H}_K} = f(x_i)$．类似地，$\langle K(\cdot, x_i), K(\cdot,x_j)\rangle_{{\cal H}_K}=K(x_i, x_j)$（${\cal H}_K$ 的再生性质），

weiya 注: 核再生性质 (kernel reproducing property)

对于任意的 $x\in {\cal X}$, $K(\cdot, x) \in \cal H$，并且满足 $\langle f, K(\cdot, x)\rangle_{\cal H} = f(x)\qquad \text{for all }f\in \cal H\,.$ 这称为 核再生性质 (kernel reproducing property)．另外，对于任意半正定核 $K$，存在唯一的希尔伯特空间 $\cal H$ 满足核再生性质，此时 $\cal H$ 也被称之为 再生核希尔伯特空间 (RKHS).

也因此对于 $f(x)=\sum_{i=1}^N\alpha_iK(x,x_i)$

$J(f)=\sum\limits_{i=1}^N\sum\limits_{j=1}^NK(x_i,x_j)\alpha_i\alpha_j\tag{5.51}\label{5.51}$

根据 \eqref{5.50} 和 \eqref{5.51}，\eqref{5.48} 退化为有限维准则

$\underset{\aalpha}{\min} L(\y,\K\aalpha)+\lambda\aalpha^T\K\aalpha\tag{5.52}\label{5.52}$

我们正在使用向量记号，其中 $\K$ 是第 $ij$ 个元素为 $K(x_i,x_j)$ 的 $N\times N$ 的矩阵．简单的数值算法可以用来优化 \eqref{5.52}．无限维问题 \eqref{5.48} 或 \eqref{5.49} 退化为有限维优化问题的现象在支持向量机（见第 12 章）中被称为 核性质 (kernel property)．

这类模型有一个贝叶斯解释，其中 $f$ 被解释为零均值平稳高斯过程的实现，其中先验协方差函数为 $K$．特征值分解得到一系列方差为 $\gamma_j$ 的正交特征函数 $\phi_j(x)$．一般的情形是，“光滑”函数 $\phi_j$ 有更大的先验方差，而“粗糙”的 $\phi_j$ 有较小的先验方差．\eqref{5.48} 中的惩罚是先验对联合概率的贡献度，并且方差越小惩罚越大（与 \eqref{5.43} 相比）．

为了简便，我们这里处理所有 $\cal H$ 中的成员都被惩罚的情形，如 \eqref{5.48}．更一般地，$\cal H$ 中可能有些组分我们希望单独留下来，比如 5.4 节中的三次光滑样条的线性函数．5.7 节的多维 thin-plate 样条以及张量积样条也都属于这类．在这些情形下，有个更方便的表示 $\cal H=\cal H_0\oplus\cal H_1$，举个例子，其中零空间 $\cal H_0$ 由没有被惩罚的 $x$ 的低阶多项式组成．惩罚项变为 $J(f)=\Vert P_1f\Vert$，其中 $P_1$ 是 $f$ 在 $\cal H_1$ 上的正交投影．这个解形式为 $f(x)=\sum_{j=1}^M\beta_jh_j(x)+\sum_{i=1}^N\alpha_iK(x,x_i)$，其中第一项表示 $\cal H_0$ 中的展开．从贝叶斯的观点看，$\cal H_0$ 中组分的系数的先验的方差无穷大．

RKHS 的例子¶

上述的机理是由核 $K$ 和损失函数 $L$ 的选择 驱动 (driven) 的．我们首先考虑采用平方误差损失的回归．将 \eqref{5.48} 中的惩罚特定为最小二乘，则解可以用对应 \eqref{5.49} 或 \eqref{5.52} 的两个等价方式进行描述：

对于无穷维的广义岭回归问题 $\underset{\{c_j\}_1^\infty}{\min}\sum\limits_{i=1}^N\Big(y_i-\sum\limits_{j=1}^\infty c_j\phi_j(x_i)\Big)^2+\lambda\sum\limits_{j=1}^\infty \frac{c_j^2}{\gamma_j}\tag{5.53}\label{5.53}$ 或者写成 $\underset{\alpha}{\min}(\y-\K\alpha)^T(\y-\K\alpha)+\lambda \aalpha^T\K\aalpha\tag{5.54}\label{5.54}$

易得 $\alpha$ 的解

$\hat\aalpha = (\K+\lambda\I)^{-1}\y\tag{5.55}\label{5.55}$

且

$\hat f(x)=\sum\limits_{j=1}^N\hat\alpha_jK(x,x_j)\tag{5.56}$

$N$ 个拟合值的向量为

$\begin{align} \hat{\f} &=\K\hat\aalpha\notag\\ &=\K(\K+\lambda\I)^{-1}\y\tag{5.57}\label{5.57}\\ &=(\I+\lambda \K^{-1})^{-1}\y\tag{5.58}\label{5.58} \end{align}$

估计值 \eqref{5.57} 也是稀疏统计 (Cressie, 1993)⁴ 中高斯随机域的 kriging 估计．另外 \eqref{5.58} 可以与光滑样条拟合 \eqref{5.17} 进行比较．

weiya 注：Recall

$\mathbf S_\lambda=(\mathbf I+\lambda \mathbf K)^{-1}\tag{5.17}\label{5.17}$

带惩罚的多项式回归¶

核 $K(x,y)=(\langle x, y\rangle+1)^d$ (Vapnik, 1996)⁵，对于 $x,y\in \IR^p$，有 $M=\binom{p+d}{d}$ 个特征函数，它张成了 $\IR^p$ 中总阶数为 $d$ 的多项式空间．举个例子，当 $p=2, d=2,M=6$，有

$\begin{align} K(x,y)&=1+2x_1y_1+2x_2y_2+x_1^2y_1^2+x_2^2y_2^2+2x_1x_2y_1y_2\tag{5.59}\\ &=\sum\limits_{m=1}^Mh_m(x)h_m(y)\tag{5.60} \end{align}$

其中

$h(x)^T=(1,\sqrt{2}x_1, \sqrt{2}x_2, x_1^2, x_2^2, \sqrt{2}x_1x_2)\tag{5.61}\label{5.61}$

可以用 $M$ 个 $K$ 的特征函数和特征值来表示 $h$

$h(x)=\V\D_\gamma^{\frac 12}\phi(x)\tag{5.62}\label{5.62}$

其中 $\D_\gamma=\diag(\gamma_1,\gamma_2,\ldots, \gamma_M)$，并且 $\V$ 是 $M\times M$ 的，且为正交．

weiya 注：

练习 5.16(a) 要求推导 \eqref{5.62}，该小问已解决，详见 Issue 164: Ex. 5.16．

假设我们希望求解带惩罚的多项式回归问题

$\underset{\{\beta_m\}_1^M}{\min}\sum\limits_{i=1}^N\Big(y_i-\sum\limits_{m=1}^M\beta_mh_m(x_i)\Big)^2+\lambda \sum\limits_{m=1}^M\beta_m^2\tag{5.63}\label{5.63}$

将 \eqref{5.62} 代入 \eqref{5.63}，我们得到 \eqref{5.53} 的展开来进行优化（练习 5.16）．

weiya 注：Ex. 5.16

已解决，详见 Issue 164: Ex. 5.16．

基函数的个数 $M=\binom{p+d}{d}$ 可以非常大，通常大于 $N$．等式 \eqref{5.55} 告诉我们如果采用解函数的核表示，我们仅仅需要对核进行 $N^2$ 次赋值，而且可以以 $O(N^3)$ 的计算量得到解．

This simplicity is not without implications. \eqref{5.61} 中的每个多项式 $h_m$ 从 $K$ 的特定形式继承了缩放因子，这对 \eqref{5.63} 的惩罚有影响．我们将在下一节详细讨论．

高斯径向基函数¶

在前面的例子中，选择核是因为能表示成多项式的展开，这样可以方便地计算高维内积．在这个例子中，选择核是因为 \eqref{5.50} 中的函数形式．

举个例子，在平方误差损失下，高斯核 $K(x,y)=e^{-\nu \Vert x-y\Vert^2}$ 能得到展开式为高斯径向基函数的回归模型，

$k_m(x)=e^{-\nu \Vert x-x_m\Vert^2},m=1,\ldots, N\tag{5.64}$

每个点都在训练特征向量 $x_m$ 处中心化了．可以采用 \eqref{5.54} 来估计参数．

图 5.13 采用第二章混合例子中的第一个坐标展示了 $\IR^1$ 中的径向核．我们展示了 $200$ 个核基函数 $k_m(x)=K(x,x_m)$ 中的五个．

图 5.14 展示了 $x\in \IR^1$ 的径向核的隐式特征空间．我们计算 $200\times 200$ 的核矩阵 $\K$，以及其特征分解 $\Phi\D_\gamma\Phi^T$．我们可以认为 $\Phi$ 的列和 $\D_\gamma$ 中对应的特征值是特征展开 \eqref{5.45} 中的经验估计．

原书脚注：

$\Phi$ 的第 $\ell$ 列是 $\phi_\ell$ 的一个估计，这是对 $N$ 个观测中的每一个进行赋值．另外，$\Phi$ 的第 $i$ 行是基函数 $\phi(x_i)$（在 $x_i$ 处取值）的估计向量．尽管原则上，$\phi$ 可以有无穷多的元素，但我们的估计至多有 $N$ 个元素．

尽管特征向量是离散的，但我们还是可以将它们表示成 $\IR^1$ 中的函数（练习 5.17）．

weiya 注：Ex. 5.17

已解决，详见 Issue 165: Ex. 5.17．

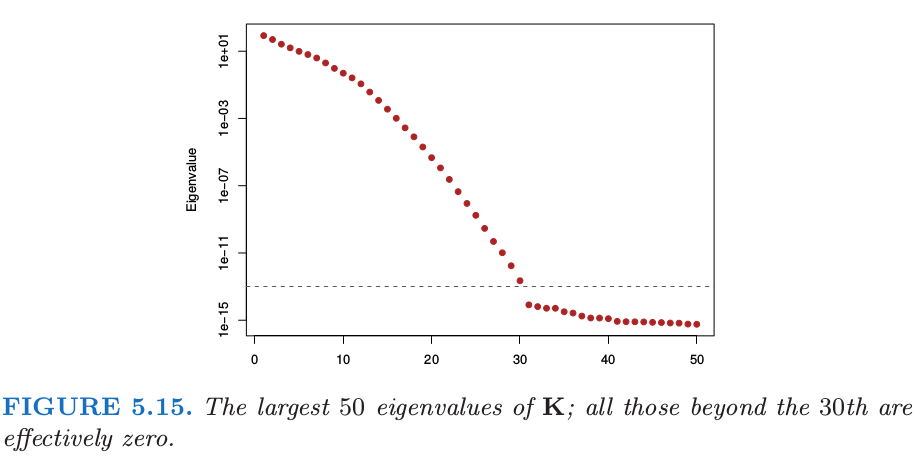
图 5.15 展示了 $\K$ 的最大的 $50$ 个特征值．最大特征值对应的特征函数是光滑的，并且它们随着 order 增加变得更加弯曲．这使得 \eqref{5.49} 中的惩罚变成了可能，其中我们看到高阶函数的系数比低阶函数惩罚更多．图 5.14 中的右面板显示了下面特征函数对应的特征空间的表示

$h_\ell(x)=\sqrt{\hat{\gamma_\ell}}\hat\phi_\ell(x),\ell=1,\ldots, N\tag{5.65}$

注意到 $\langle h(x_i), h(x_{i’})\rangle=K(x_i, x_{i’})$．通过特征值来缩放快速将大部分的函数降为 $0$，在这种情形下留下大约 $12$ 个有效维度．对应的优化问题是如 \eqref{5.63} 中标准的岭回归．所以尽管原则上隐式的特征空间是无穷维的，但有效维度还是非常小的，因为对每个基函数应用相对大小的收缩．核缩放参数 $\nu$ 在这里也起一定作用；更大的 $\nu$ 意味着更多局部的 $k_m$ 函数，并且也增加了特征空间的有效维度．更多细节参见 Hastie and Zhu (2006)⁶．

我们知道被称为 thin-plate 样条 (5.7 节)是关于径向基函数的展开 (Girosi et al., 1995)¹，它由下列核产生

$K(x, y)=\Vert x-y\Vert^2\LOG(\Vert x-y\Vert)\tag{5.66}$

径向基函数将在 6.7 节详细讨论．

支持向量机¶

第 12 章中用于两个类别分类的支持向量机有形式 $f(x)=\alpha_0+\sum_{i=1}^N\alpha_iK(x,x_i)$，选择参数使下式最小化

$\underset{\alpha_0,\aalpha}{\min}\Big\{ \sum\limits_{i=1}^N[1-y_if(x_i)]_+ + \frac{\lambda}{2}\aalpha^T\K\aalpha \Big\} \tag{5.67}\label{5.67}$

其中 $y_i\in \{-1, 1\}$，并且 $[z]_+$ 记做 $z$ 的正值部分．这可以看成是带线性约束的二次优化问题，并要求该解的二次规划算法．支持向量 (support vector) 的名字来自这样一个事实：一般有许多的$\hat\alpha_i=0$【因为 \eqref{5.67} 中损失函数的 piecewise-zero 特性】，也因此 $\hat f$ 是 $K(\cdot, x_i)$ 的子集的展开．更多细节见 12.3.3节．

Girosi, F., Jones, M. and Poggio, T. (1995). Regularization theory and neural network architectures, Neural Computation 7: 219–269. ↩↩↩
Wahba, G. (1990). Spline Models for Observational Data, SIAM, Philadelphia. ↩↩
Evgeniou, T., Pontil, M. and Poggio, T. (2000). Regularization networks and support vector machines, Advances in Computational Mathematics 13(1): 1–50. ↩
Cressie, N. (1993). Statistics for Spatial Data (Revised Edition), Wiley-Interscience, New York. ↩
Vapnik, V. (1996). The Nature of Statistical Learning Theory, Springer, New York. ↩
Hastie, T. and Zhu, J. (2006). Discussion of “Support vector machines with applications” by Javier Moguerza and Alberto Munoz, Statistical Science 21(3): 352–357. ↩