6.2 选择核的宽度¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2017-03-01 |
| 更新 | 2018-07-18 |
| 状态 | Done |
在每个核 $K_\lambda$ 中,$\lambda$ 为控制宽度的参数:
- 对于有度量宽度的 Epanechnikov 或三次立方核,$\lambda$ 为支撑域的半径.
- 对于高斯核,$\lambda$ 为标准差.
- $\lambda$ 为 $k$-最近邻中最近邻的数目 $k$,经常表达成分数或者整个训练样本的跨距 $k/N$.
当我们改变平均窗口的宽度,存在很自然的偏差和方差之间的权衡 (bias-variance tradeoff),对于局部平均是最显然的:
- 如果窗口较窄,$\hat f(x_0)$ 是离 $x_0$ 近的一小部分 $y_i$ 值的平均,则它的方差相对较大——与单个 $y_i$ 的方差相近.偏差会趋向于较小,这是因为 $\E(y_i)=f(x_i)$ 中的每一个应该与 $f(x_0)$ 相近.
- 如果窗口较宽,$\hat f(x_0)$ 的方差相对于任意 $y_i$ 的方差较小,这是因为平均的效应.偏差会较高,因为我们现在采用的是与 $x_0$ 离得较远的观测 $x_i$,而且不保证 $f(x_i)$ 离 $f(x_0)$ 较近.
相似的结论可以应用到局部回归估计,比如局部线性:当宽度趋于 $0$,估计量则近似为对训练数据插值得到的分段线性函数;当宽度趋于无穷大,则拟合值近似为对数据的整体最小二乘拟合.
weiya 注:Recall
这里应用第五章中选择光滑样条的正规化参数的讨论.局部回归光滑器是线性估计器;$\mathbf{\hat f=S_\lambda y}$ 中的光滑矩阵由等价核 \eqref{6.8} 构成,并且第 $ij$ 个元素值为 ${\mathbf S_\lambda}_{ij}=l_{i}(x_{j})$.舍一法交叉验证特别地简单(练习 6.7),广义交叉验证,$C_p$(练习 6.10),以及 $k$ 折交叉验证也很简单.有效自由度再一次定义为 $\trace(\mathbf S_\lambda)$,并且可以用来校准光滑的程度.
weiya 注:Ex. 6.7
已解决,详见 Issue 150: Ex. 6.7.
weiya 注:Ex. 6.10
已解决,详见 Issue 151: Ex. 6.10.
图 6.7 比较了光滑样条和局部线性回归的等价核.局部线性光滑器有 $40\%$ 的跨度 (span),得到 $df=\trace(\mathbf S_\lambda)=5.86$.光滑样条进行校准后得到同样的 $df$,并且它们的等价核非常相似.
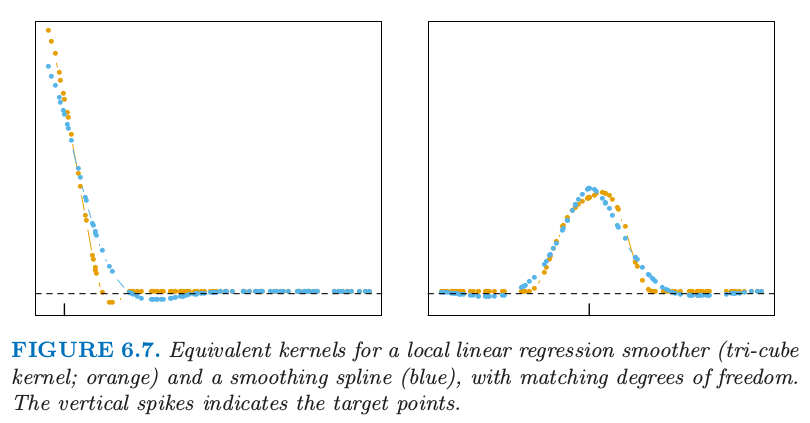
图 6.7.相同自由度下, 局部线性回归光滑器的等价核(三次立方核;橘黄色)以及光滑样条(蓝色).竖直的钉表示目标点.