10.12 正则化¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2017-10-09 |
| 更新 | 2020-01-10 11:30:03 |
| 状态 | Done |
除了候选树的大小 $J$,梯度 boosting 的另一个元参数 (meta-parameter) 是 boosting 的迭代次数 $M$.每一次迭代通常会降低训练风险 $L(f_M)$,所以对于充分大的 $M$,误差可以达到任意小.然而,对训练数据拟合得太好会导致过拟合,它会降低预测未来数据的效果.因此,存在一个最小 化未来预测风险的最优大小 $M^*$,它依赖于具体应用.估计 $M^*$的一种方便方式是在验证样本上将预测风险看成是关于 $M$ 的函数.最小化风险的 $M$ 值则作为 $M^*$ 的一个估计.这类似于经常用在神经网络中的 早停 (early stopping) 策略(11.4 节).
收缩¶
控制 $M$ 的值并不是唯一正则化的策略.与岭回归和神经网络一样,也可以应用收缩策略(见 3.4.1 节和 11.5 节).Boosting 中收缩最简单的实现方式是使用因子 $0 < \nu < 1$ 来收缩每棵树的贡献.也就是,算法 10.3 的第 2(d) 行用下式代替
参数 $\nu$ 可以看成是控制 boosting 过程的学习速率.较小的 $\nu$(更多的收缩)会导致同样大小的迭代次数 $M$ 下更大的训练风险.因此,$\nu$ 和 $M$ 都控制了训练数据的预测风险.然而,这些参数并不单独作用.对于同样的训练风险较小的 $\nu$ 会导致较大的 $M$,所以它们之间存在权衡.
经验上,(Friedman, 20011) 已经发现较小的 $\nu$ 会得到更好的测试误差,并且需要更大的 $M$ 与之对应.事实上,最好的策略是将 $\nu$ 设得很小($\nu < 0.1$),然后通过 早停 (early stopping) 来选择 $M$.这会给回归和概率估计带来重大的改善(与没有收缩时相比,$\nu = 1$).通过 \eqref{10.20} 式改善对应的误分类风险虽然很小,但是仍然显著.
Recall
这个改善需要以计算量为代价:较小的 $\nu$ 得到较大的 $M$,并且计算量与后者成比例.然而,将在下面看到,许多迭代的计算即使是在非常大的数据集上也是可行的.部分原因是每一步生成的树是没有剪枝的.
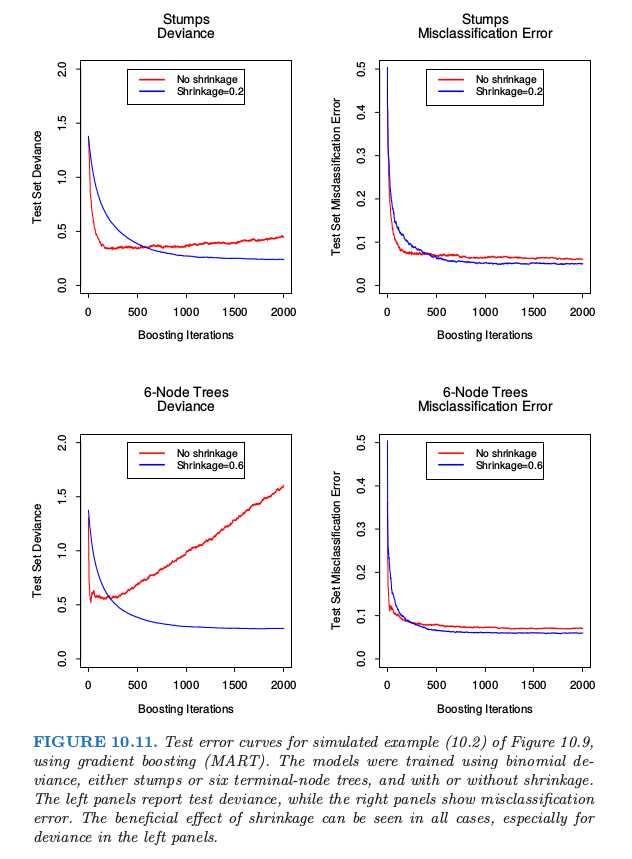
图 10.11 显示了图 10.2 的模拟例子 \eqref{10.2} 的测试误差曲线.
Recall: \eqref{10.2}
Gradient boosted 模型(MART)通过采用二项偏差来训练,分 stump 和 6 个终止结点树的情况讨论,以及分有无收缩进行讨论.收缩的好处是很显然的,特别是当跟踪二项偏差时.有了收缩,每个测试误差曲线达到较低的值,并且在许多迭代中保持不变.
16.2.1 节将 boosting 的向前逐步收缩和为了正则化模型参数使用的 $L_1$ 惩罚(lasso)联系起来.我们认为 $L_1$ 惩罚可能会比用在一些方法(比如支持向量机)中的 $L_2$ 惩罚要更好.
子采样¶
我们在 8.7 节看到bootstrap averaging (bagging) 通过 averaging 提高了噪声分类器的表现效果.第 15 章详细讨论了通过平均实现的降低方差的机制.我们也可以在gradient boosting 中采用这一方法,同时提高了效果和计算效率.
采用 stochastic gradient boosting (Friedman, 19992),在每一步我们采样 $\eta$ 倍的训练观测值(无放回),并且采用这种子采样来生成下一棵树.剩下的算法同样.一般可以取 $\eta$ 为 $\frac{1}{2}$,尽管对于大的 $N$,$\eta$ 可以比 $\frac{1}{2}$ 小很多.
这种采样不仅仅降低了 $\eta$ 倍的计算时间,在很多情况下也实际上得到了更精确的模型.
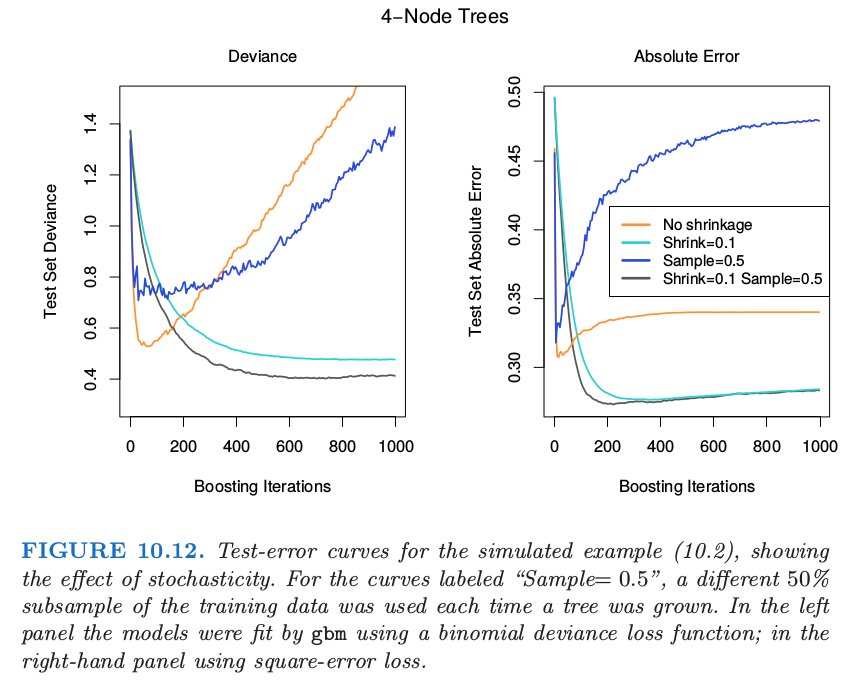
图 10.12 说明了采用模拟例子 \eqref{10.2} 的子采样的效果,既可以看成是分类的例子,也可以看成是回归的例子.我们看到这两种情形下,采用收缩的的子采样比剩下的表现要好.似乎没有收缩的子采样会表现得很差.
缺点是我们现在需要设置四个参数:$J,M,\nu$ 和 $\eta$.一般地,通过前期的尝试确定合适的 $J,\nu$ 和 $\eta$,将 $M$ 留作主要的参数.
weiya 注:
Gradient Boosting regularization – scikit-learn 比较了不同学习速率 $\nu$ 和子采样 $\eta$ 在例 \eqref{10.2} 上的表现,
