6.3 $\IR^p$中的局部回归¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2017-03-01 |
| 更新 | 2025-12-30 |
| 状态 | Done |
核光滑和局部回归可以非常自然地推广到二维或更高维空间中.Nadaraya–Watson 核光滑器局部拟合常值,其中权重由 $p$ 维核得到.局部线性回归通过加权最小二乘来拟合 $X$ 中局部的超平面,参数由 $p$ 维核给出.这可以很简单地实现,并且一般偏爱边界处有更好的表现的局部常值拟合.
令 $b(X)$ 为 $X$ 最大 degree 为 $d$ 的多项式的向量.例如,$d=1,p=2$ 时有 $b(X)=(1,X_1,X_2)$;$d=2$ 时我们得到 $b(X)=(1,X_1,X_2,X_1^2,X_2^2,X_1X_2)$;并且在 $d=0$ 的平凡情形下我们得到 $b(X)=1$.在每个 $x_0\in \IR^p$ 处求解 得到拟合 $\hat f(x_0)=b(x_0)^T\hat \beta(x_0)$.一般地,核是径向函数,比如 radial Epanechnikov 或三次立方核 其中 $\Vert \cdot\Vert$ 是欧几里得范数.因为欧式范数取决于每个坐标的单位,所以对每个预测变量进行标准化是有意义的,举个例子,在光滑之前,标准化为单位标准误差.
边界影响不仅在一维光滑中是一个问题,在二维或者高维空间中是更大的问题,因为边界上点的比例较大.事实上,维数灾难的一个表现是边界点的比例随着维数的增大而增大.直接修改核来适应二维边界会变得很复杂,特别是对于不规则的边界.局部多项式回归完美地将任意维度中边界矫正为需要的阶数.图 6.8 显示了在天文研究中一些测量值上的局部线性回归,其中用了不常见的预测变量设计(星形).这里边界特别不规则,并且当我们接近边界时拟合表面必须在数据稀疏度的区域中插值.
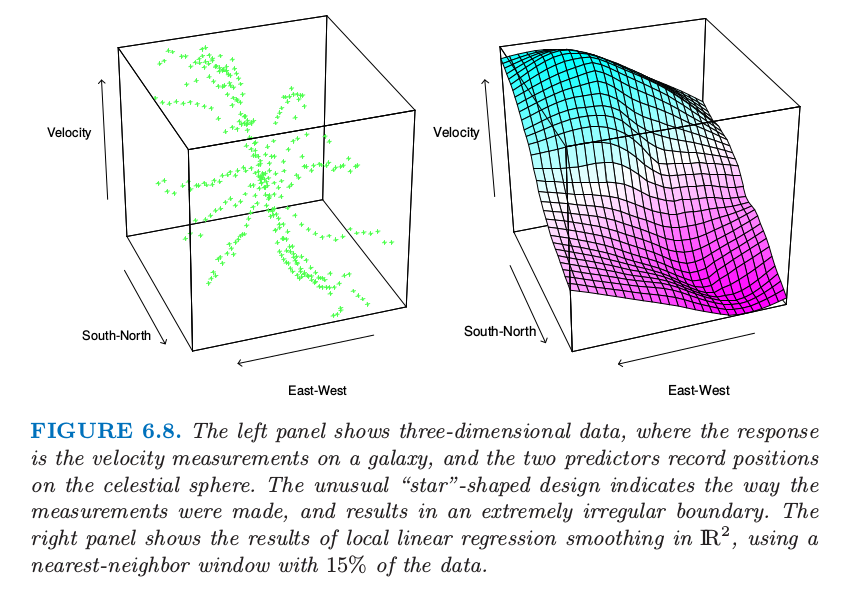
图 6.8. 左图显示了三维数据,其中响应变量为星系速度的测量值,两个预测变量记录了在宇宙中的位置.特别的星形设计表示衡量的方式,而且最终得到非常不规则的边界.右图显示了在 $\IR^2$ 中局部线性拟合的结果,采用含 $15\%$ 数据的最近邻窗口.
局部回归在高于 $2$ 或 $3$ 维中不是很有用.例如,在第 $2$ 章中,我们已经详细讨论了维数的问题.当维数增加时,同时维持局部(低偏差)并且邻域中相当大规模的样本是不可能的,总体数据大小没有随着 $p$ 指数增长.$\hat f(X)$ 的可视化在高维中会变得困难,并且这通常是光滑的其中一个主要目标.尽管图 6.8 中的 散点云 (scatter-cloud) 和 线框图 (wire-frame) 看起来很吸引人,但除了在总量水平下,结果的解释是很困难的.从数据分析的角度,条件图象更有用.
图 6.9 显示了三个预测变量的一些环境数据的分析.这里的网格显示出了在其他两个变量,温度和风速的条件下,臭氧作为辐射的函数.然而,在某变量的值的条件下意味着确实表明对这个值是局部的(正如在局部回归中一样).图 6.9 中的每个图是在该图中在每个条件值下显示出值的范围.在图本身,显示了数据子集(响应变量相对于剩余变量),以及一个对数据的一维局部线性回归.尽管当观察拟合的 3 维表明不是完全一样的,但可能对理解数据的联合行为是有用的.
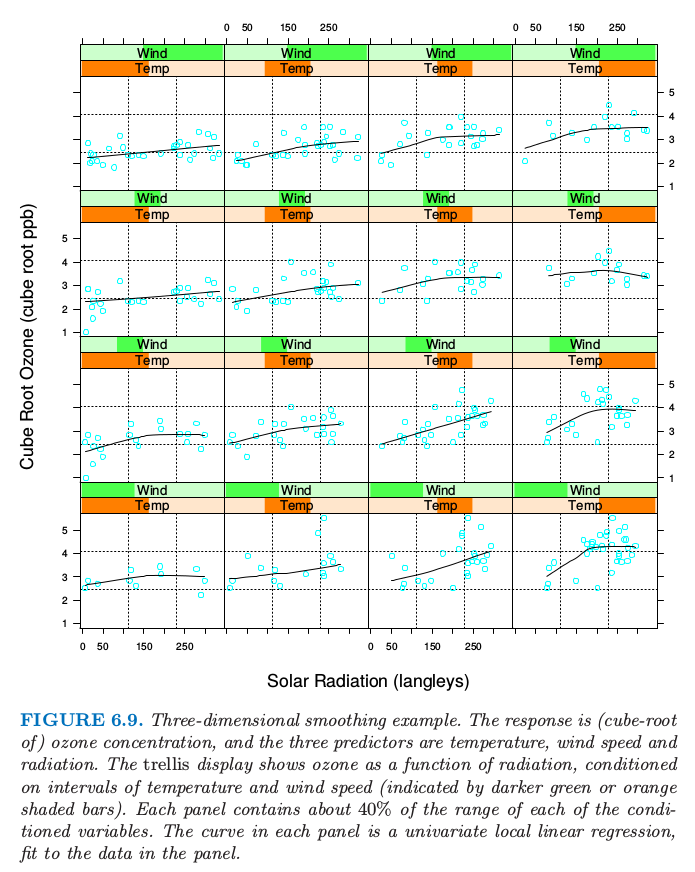
图 6.9. 三维光滑例子.响应变量是臭氧浓度(立方根),并且这三个预测变量分别是温度,风速和辐射.网格显示了在温度区间和风速条件下(由深绿或橘黄阴影条表示)臭氧浓度作为辐射的函数.每个图包含每个条件变量大概 $40\%$ 的区间.每个图中的曲线是对图中数据的单变量局部线性回归拟合.
weiya 注:
已重现图 6.9,详见 Reproduce Figures with Lattice