算法:Alg. 17.1¶
| 原文 | 17.3 连续变量的无向图模型 |
|---|---|
| 作者 | szcf-weiya |
| 发布 | 2018-06-15 |
| 更新 | 2018-07-08 |
这篇笔记记录了用 R 语言实现算法 17.1 并应用到实际数据的具体过程。
实现过程¶
具体细节详见 17.3 连续变量的无向图模型,这里只贴出算法:

这个算法是针对图模型结构已知的情形。对于 2(b) 中的 “reduced system of equations”,我们需要根据具体模型缺失边的情况来确定出
对于书中给出的例子
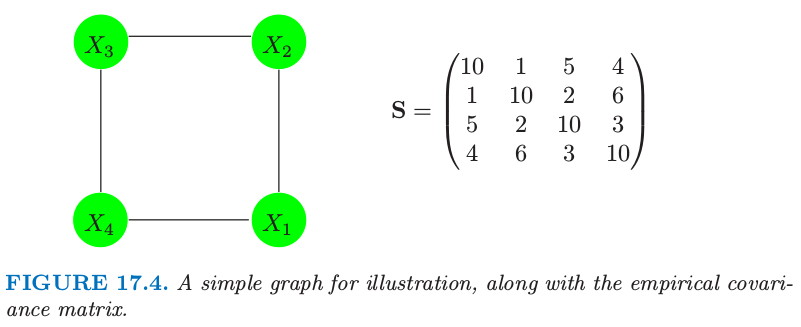
根据具体缺失边的情况,分别给出 $\mathbf W^*_{11}$ 和 $s_{12}^*$:
## W11.star, s12.star based on the known graph structure
if (j == 1)
{
W.11.star = W[-c(1,3), -c(1,3)]
s.12.star = S[1, -c(1,3)] # edge 1-3
}
else if (j == 2)
{
W.11.star = W[-c(2,4), -c(2,4)]
s.12.star = S[2, -c(2,4)] # edge 2-4
}
else if (j == 3)
{
W.11.star = W[-c(3,1), -c(3,1)]
s.12.star = S[3, -c(1,3)] # edge 3-1
}
else if (j == 4)
{
W.11.star = W[-c(2,4), -c(2,4)]
s.12.star = S[4, -c(2,4)] # edge 2-4
}
为了让程序更有适用性,我们采用邻接矩阵来表示边的缺失,则上面代码可以简化为
adj = matrix(c(0, 1, 0, 1,
1, 0, 1, 0,
0, 1, 0, 1,
1, 0, 1, 0), ncol = 4)
## use adjacency matrix
edge.idx = which(adj[j,] != 0)
W.11.star = W[edge.idx, edge.idx]
s.12.star = S[j, edge.idx]
更新 $w_{12}$,
## solve reduced system of equations
beta.star = solve(W.11.star, s.12.star)
## update
if (j == 1 || j == 4)
{
beta.hat[-2] = beta.star
}
else if (j == 2)
{
beta.hat[-3] = beta.star
}
else if (j == 3)
{
beta.hat[-1] = beta.star
}
W.reorder[p, -p] = W.11 %*% beta.hat
W.reorder[-p, p] = W.11 %*% beta.hat
W.backup = W
W = W.reorder[order(idx), order(idx)]
采用邻接矩阵,计算 beta.hat 的代码可以简化为
beta.hat.add.j = matrix(rep(0,p),ncol=1)
beta.hat.add.j[edge.idx] = beta.star
beta.hat = beta.hat.add.j[-j]
当 $\mathbf W$ 收敛后,计算 $\hat{\mathbf\Sigma} ^{-1}$:
## final cycle
if (finalcycle)
{
theta22 = 1/(S[j, j] - sum(W.reorder[p,-p]*beta.hat))
theta12 = -1.0 * beta.hat * theta22
Omega[j, j] = theta22
Omega[j, -j] = theta12
Omega[-j, j] = theta12
}
个人感觉整个实现过程需要特别注意算法中 2(b) 步的 “reduced system of equations”,我们是要删去还有缺失边的信息,因为根据式 (17.12) 缺失边会有额外的拉格朗日常数惩罚
完整代码参见 GitHub。
结果¶
运行结果如下:
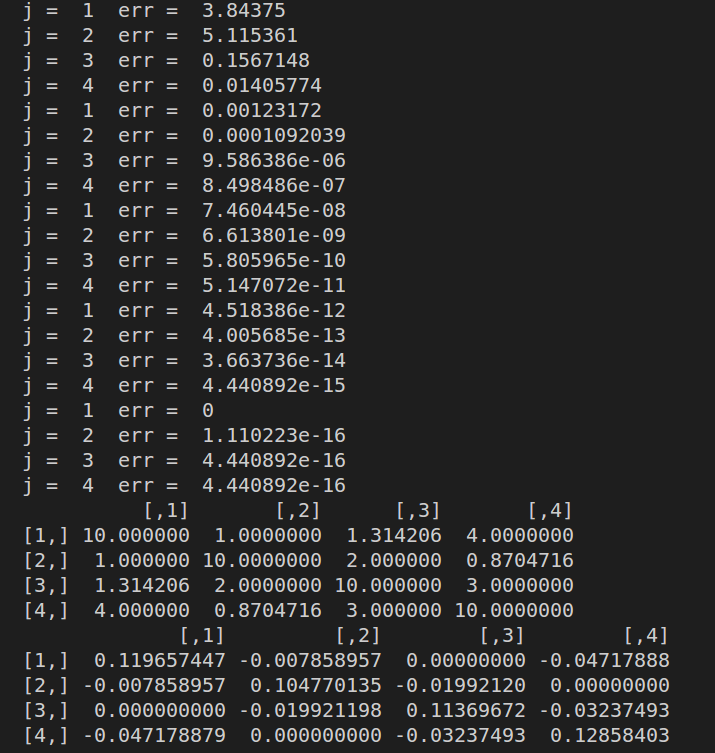
可以发现与书中的结果是一致的