$\IR^p$中结构化局部回归¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2016-09-30 |
| 更新 | 2025-12-30 |
当维度与样本大小的比率不是很好,则局部回归对我们没有太大帮助,除非我们想要对模型做出一些结构化的假设.这本书的很多部分是关于结构化回归和分类模型的.这里我们关注一些与核方法直接相关的方法.
结构核¶
weiya 注:Recall
一种方式是修改核.默认的球面核 \eqref{6.13} 对每个坐标给出了相等的权重,所以一种自然的默认策略是对每个变量标准化得到单位标准误差.更一般的方式是使用半正定矩阵 $\mathbf A$ 来对不同的坐标进行赋予权重:
整个坐标或者方向的影响可以通过在 $\mathbf A$ 上加入合适的限制来降低或者忽略.举个例子,如果 $\mathbf A$ 为对角矩阵,则我们可以通过增加或者减小 $A_{jj}$ 来增大或者减小单个预测变量 $X_j$ 的影响.预测变量很多通常都是高度相关的,比如从相似的数字信号或者图像中得到.预测变量的协方差函数可以用来修改矩阵 $\mathbf A$,使得在高频对比中关注更少(练习 6.4).研究者们已经提出了多维核参数训练的方法.举个例子,第 11 章中讨论的投影寻踪回归模型是合适的,其中 $\mathbf A$ 的低阶形式表示 $\hat f(X)$ 的岭回归.关于 $\mathbf A$ 的更一般的模型是很复杂的,相反地,我们倾向于接下来讨论的结构形式的回归函数.
结构回归函数¶
我们试着在 $\IR^p$ 中拟合回归函数 $\E(Y\mid X)=f(X_1,X_2,\ldots,X_p)$,其中每一阶的交叉项都可能存在.很自然地可以考虑下列形式的方差分析 (ANOVA) 分解:
并且接着引入消除一些高阶项的结构.可加性模型假设只有主要影响项 $f(X)=\alpha+\sum\limits_{j=1}^pg_j(X_j)$,二阶模型会有次数至多为 2 的交叉项,以此类推.在第 9 章中,我们描述了对于拟合这样低阶交叉模型的 迭代向后拟合 (iterative backfitting) 算法.在加性模型中,举个例子,如果所有但除了第 $k$ 项是已知的,则我们可以用 $Y-\sum_{j\neq k}g_j(X_j)$ 在 $X_k$ 上的局部回归来估计 $g_k$.这个依次对每个函数重复进行,直到收敛.重要的细节是,在每一步,一维局部回归是所有都需要的.同样的思想可以用来拟合低维 ANOVA 分解.
这些结构模型的一个重要的特殊情形是 可变系数模型 (varying coefficient models) 类.举个例子,假设我们将 $X$ 中的 $p$ 个预测变量分成集合 $(X_1,X_2,\ldots,X_q),q < p$,剩下的变量放进向量 $Z$ 中.接着我们假设条件线性模型
对于给定的 $Z$,这是线性模型,但是每个参数可以随着 $Z$ 而改变.很自然地可以通过局部加权最小二乘拟合这个模型:
图 6.10 说明了在人类大动脉测量数据上的想法.一个由来已久的说法是 大动脉 (aorta) 会随着 age 增长而变厚.这里我们将大动脉的 diameter 建立为 age 的线性函数,但是允许系数随着 gender 和 depth 的变化而变化.我们对男性和女性分别采用局部回归模型.尽管大动脉确实很明显地(在大动脉比较厚区域中)随着年龄而变厚,这种关系随着到大动脉的距离而减弱.图 6.11 显示了截距和斜率作为深度的函数.
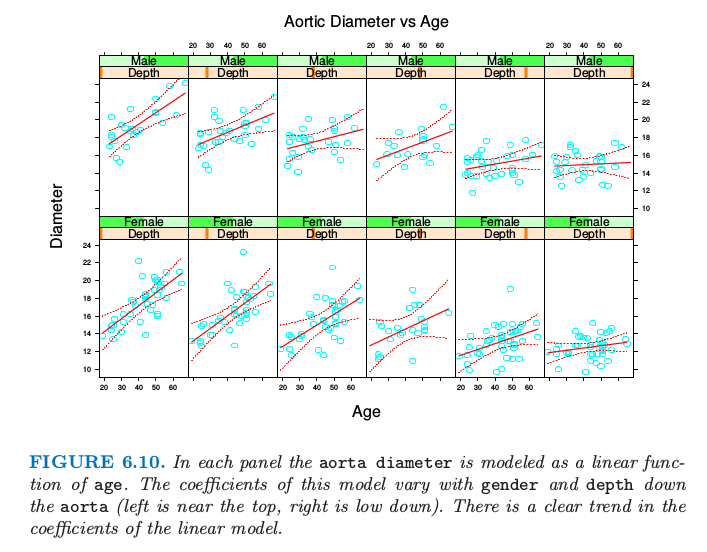
图 6.11. 每张图中
aorta diameter建立为age的线性函数模型.这个模型的系数随着gender和到aorta的depth(左边靠近顶端,右边靠近底端)变化.在线性模型中的系数有着明显的趋势.
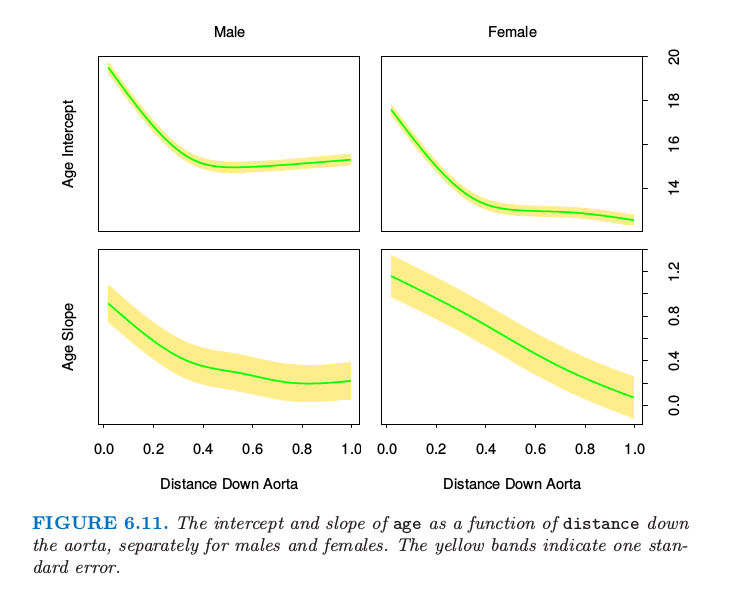
图 6.11. 在男性和女性情形下,
age作为到 aorta 的distance的函数的截距和斜率.黄色带状表示一个标准误差.