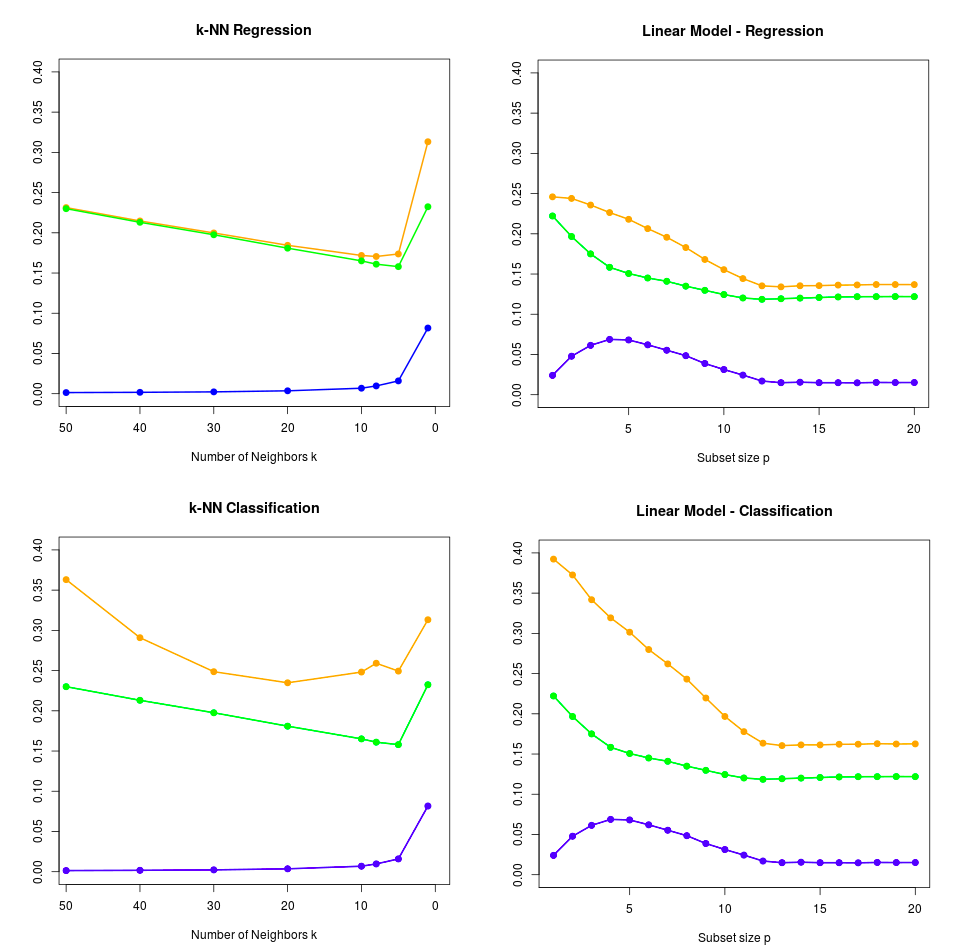


模拟：Fig. 7.3¶

R Notebook	模拟：Fig. 7.3
作者	szcf-weiya
发布	2018-01-06
更新	2018-02-04

本笔记是ESL7.3节图7.3的模拟。

生成数据¶

# generate dataset
genX <- function(n = 80, p = 20){
  X = matrix(runif(n*p, 0, 1), ncol = p, nrow = n)
  return(X)
}
# generate response
genY <- function(X, case = 1){
  n = nrow(X)
  Y = numeric(n)
  if (case == 1){ # for the left panel of fig. 7.3
    Y = sapply(X[, 1], function(x) ifelse(x <= 0.5, 0, 1))
  }
  else {
    Y = apply(X[, 1:10], 1, function(x) ifelse(sum(x) > 5, 1, 0))
  }
  return(Y)
}
## global parameters setting
ntest = 1000
percent = 0.75
B = 100 # the number of repetition

左图情形： kNN回归和分类¶

首先考虑左图的情形: 若$X_1\le 1/2$，$Y=0$，且若$X_1>1/2$，$Y=1$，而且应用$k$-最近邻模型。

设置随机种子，方便后面进行随机化。

# case 1
seed = 123
set.seed(seed)
X = genX()
Y = genY(X)
X.test = genX(n = 1000)
Y.test = genY(X.test)

下面编写主程序，变化$k$最近邻中的邻居数$k$，并重复建立$B$次模型用来估计测试集中的每个点，用来估计其偏差、方差及预测误差的期望。

## kNN
library(class)
library(caret)
n = nrow(X)
K = 50 # the maximum of k
# sequence of k
kseq = c(seq(K, 10, by = -10), 8, 5, 1)
nk = length(kseq)
reg.bias2.full = numeric(nk)
reg.variance.full = numeric(nk)
reg.epe.full = numeric(nk)
cl.bias2.full = numeric(nk)
cl.variance.full = numeric(nk)
cl.epe.full = numeric(nk)
for(i in 1:nk){
  reg.pred = matrix(nrow = nrow(X.test), ncol = B)
  cl.pred = matrix(nrow = nrow(X.test), ncol = B)
  for (j in c(1:B)) { # subsampling B training dataset
    train.id = sample(n, n*percent)
    X.train = X[train.id, ]
    Y.train = Y[train.id]
    # for regression
    fit1 = knnreg(X.train, Y.train, k = kseq[i])
    reg.pred[, j] = predict(fit1, X.test)
    # for classification
    #fit2 = knn(X.train, X.test, Y.train, k = kseq[i])  # levels: 0 1
    #cl.pred[, j] = as.numeric(fit2) - 1 # val: 1 2
    cl.pred[, j] = sapply(reg.pred[, j], function(x) ifelse(x>0.5, 1, 0))
  }
  ## regression squared loss
  # bias
  bias2 = (rowMeans(reg.pred) - Y.test)^2
  # variance
  variance = apply(reg.pred, 1, function(x) var(x))
  # expected prediction error
  epe = sapply(1:nrow(X.test), function(i) mean((reg.pred[i, ]-Y.test[i])^2))
  # mean
  reg.bias2.full[i] = mean(bias2)
  reg.variance.full[i] = mean(variance)
  reg.epe.full[i] = mean(epe)
  ## classification 0-1 loss
  bias2 = (rowMeans(cl.pred) - Y.test)^2
  variance = apply(cl.pred, 1, function(x) var(x))
  epe = sapply(1:nrow(cl.pred), function(i) mean(cl.pred[i,]!=Y.test[i]))
  cl.bias2.full[i] = mean(bias2)
  cl.variance.full[i] = mean(variance)
  cl.epe.full[i] = mean(epe)
}

下面类似书中的图7.3，作出如下图象

## plot
yrange = 0.4
## kNN regression
#yrange = round(range(reg.epe.full)[2]+0.1, digits = 2)
plot(kseq, seq(0, yrange, length.out = nk), "n",
     xlab = "Number of Neighbors k", ylab = "", main = "k-NN Regression",
     xaxt='n', yaxt = 'n')
axis(1, at = seq(0, 50, by = 10), labels = seq(50, 0, by = -10))
axis(2, at = seq(0, yrange, by = 0.05))
lines(50-kseq, reg.epe.full, type="o", pch = 19, lwd = 2, col="orange")
lines(50-kseq, reg.bias2.full, type = "o", pch = 19, lwd = 2, col = "green")
lines(50-kseq, reg.variance.full, type = "o", lwd = 2, pch = 19, col = "blue")

## kNN classification
#yrange = round(range(cl.epe.full)[2]+0.1, digits = 2)
plot(kseq, seq(0, yrange, length.out = nk), "n",
     xlab = "Number of Neighbors k", ylab = "", main = "k-NN Classification",
     xaxt='n', yaxt = 'n')
axis(1, at = seq(0, 50, by = 10), labels = seq(50, 0, by = -10))
axis(2, at = seq(0, yrange, by = 0.05))
lines(50-kseq, cl.epe.full, type="o", pch = 19, lwd = 2, col="orange")
lines(50-kseq, reg.bias2.full, type = "o", pch = 19, lwd = 2, col = "green")
lines(50-kseq, reg.variance.full, type = "o", lwd = 2, pch = 19, col = "blue")
#lines(50-kseq, cl.bias2.full, type = "o", pch = 19, lwd = 2, col = "green")
#lines(50-kseq, cl.variance.full, type = "o", lwd = 2, pch = 19, col = "blue")

对比原图，发现除了kNN分类的预测误差的估计随$k$的变化略有不同外（也仅仅在$k$比较大的情形），其余曲线都很好地重现了原图的特征。

右图情形：最优子集回归¶

若$\sum_{j=1}^{10}X_j>5$，$Y=1$，否则$Y=0$，且采用大小为$p$的最优子集回归。

首先生成模拟数据

## case 2
seed = 123
set.seed(seed)
X = genX()
Y = genY(X, case = 2)
X.test = genX(n = ntest)
Y.test = genY(X.test, case = 2)

采用leaps包中的regsubsets函数进行最优子集回归，因为该类没有对应predict函数，于是编写自己的预测函数。需要说明的是，下面程序前半段有考虑是否存在截距项，但后来发现其实截距项是默认存在的，所以后半段没有继续考虑，简化了程序。

## use leaps package to do best subset selection
library(leaps)
## predict test dataset by using the best subset model with size p
predict.regsub <- function(model, p, X.test){
  which = summary(model)$which
  coef.raw = coef(model, p)
  # construct coef vector
  if (length(coef.raw) == p+1)
  {
    coef.vec = numeric(1+ncol(X.test)) # include intercept
    coef.vec[1] = coef.raw[1]
    flag = 1
  }
  else
  {
    coef.vec = numeric(ncol(X.test))
    flag = 0
  }
  j = flag + 1 # point to raw coef
  for (i in c(1:ncol(X.test)) + flag){
    if (which[p, i]){
      coef.vec[i] = coef.raw[j]
      j = j + 1
    }
  }
  # for simplicity, consider intercept; and in fact, every regsubset models have intercept
  pred = apply(cbind(1, X.test), 1, function(x) sum(x*coef.vec))
  return(pred)
}

接着在不同大小的子集模型下，重复建立模型对测试集进行预测，并存储预测值。

n = nrow(X)
## store all prediction
reg.pred.full = vector("list", 20)
for (i in 1:20){
  reg.pred.full[[i]] = matrix(nrow = nrow(X.test),
                              ncol = B)
}
for (i in 1:B){
  train.id = sample(n, n*percent)
  X.train = X[train.id, ]
  Y.train = Y[train.id]
  reg.sub = regsubsets(X.train, Y.train, nvmax = 20)
   for (j in 1:20){
     reg.pred.full[[j]][, i] = predict.regsub(reg.sub, j, X.test)
   }
}

下面计算平方偏差、方差和预测误差，注意回归跟分类的差别仅在于预测误差。

## calculate bias2, variance, epe
reg.bias2.full = numeric(20)
reg.variance.full = numeric(20)
reg.epe.full = numeric(20)
cl.epe.full = numeric(20)

for (i in 1:20){
  bias2 = sapply(1:ntest, function(j) (mean(reg.pred.full[[i]][j, ]) - Y.test[j])^2)
  variance = apply(reg.pred.full[[i]], 1, function(x) var(x))
  # for regression
  epe = sapply(1:ntest, function(j) mean((reg.pred.full[[i]][j, ] - Y.test[j])^2))
  # for classification
  epe.cl = numeric(ntest)
  for (j in 1:ntest)
  {
    tmp = reg.pred.full[[i]][j, ]
    cl.pred = sapply(tmp, function(x) ifelse(x > 0.5, 1, 0))
    # 0-1 loss
    epe.cl[j] = mean(cl.pred!=Y.test[j])
  }
  reg.variance.full[i] = mean(variance)
  reg.bias2.full[i] = mean(bias2)
  reg.epe.full[i] = mean(epe)
  cl.epe.full[i] = mean(epe.cl)
}

作出图象

## plot
yrange = 0.4
## best subset regression
#png(paste0("sub-reg-", seed,".png"))
#yrange = round(range(reg.epe.full)[2]+0.1, digits = 2)
plot(1:20, seq(0, yrange, length.out = 20), "n",
     xlab = "Subset size p", ylab = "", main = "Linear Model - Regression",
     xaxt='n', yaxt = 'n')
axis(1, at = seq(0, 20, by = 5), labels = seq(0, 20, by = 5))
axis(2, at = seq(0, yrange, by = 0.05))
lines(1:20, reg.epe.full, type="o", pch = 19, lwd = 2, col="orange")
lines(1:20, reg.bias2.full, type = "o", pch = 19, lwd = 2, col = "green")
lines(1:20, reg.variance.full, type = "o", lwd = 2, pch = 19, col = "blue")
#dev.off()

## best subset regression for classification
#png(paste0("sub-cl-", seed,".png"))
#yrange = round(range(reg.epe.full)[2]+0.1, digits = 2)
plot(1:20, seq(0, yrange, length.out = 20), "n",
     xlab = "Subset size p", ylab = "", main = "Linear Model - Classification",
     xaxt='n', yaxt = 'n')
axis(1, at = seq(0, 20, by = 5), labels = seq(0, 20, by = 5))
axis(2, at = seq(0, yrange, by = 0.05))
#lines(1:20, reg.epe.full, type="o", pch = 19, lwd = 2, col="orange")
lines(1:20, cl.epe.full, type="o", pch = 19, lwd = 2, col="orange")
lines(1:20, reg.bias2.full, type = "o", pch = 19, lwd = 2, col = "green")
lines(1:20, reg.variance.full, type = "o", lwd = 2, pch = 19, col = "blue")
#dev.off()

总结¶

最后我们得到的图象如下图

模拟：Fig. 7.3¶

生成数据¶

左图情形： kNN回归和分类¶

右图情形：最优子集回归¶

总结¶

Comments