10.11 大小合适的boosting树¶
| 原文 | The Elements of Statistical Learning |
|---|---|
| 翻译 | szcf-weiya |
| 发布 | 2017-10-07 |
| 更新 | 2020-01-14 18:36:02 |
| 状态 | Done |
曾经,boosting 被认为是一种将模型结合起来(combing models)的技巧,在这里模型是树.同样地,生成树的算法可看成是产生用于 boosting 进行结合的模型的 原型(primitive).这种情形下,在生成树的时候以通常的方式分别估计每棵树的最优大小(9.2 节).首先诱导出非常大(过大的)的一棵树,接着应用自下而上的过程剪枝得到估计的最优终止结点个数的树.这种方式隐含地假设了每棵树是式 \eqref{10.28} 中的最后一棵.
Recall
, 详见 10.9 节.
除了真正的最后一棵树,这显然是个很差的假设.结果导致树都趋向于很大,特别是前几步迭代中.这显著降低了模型的效果,并且增大了计算量.
避免这个问题最简单的策略是将所有树限制为相同的大小, $J_m=J\;\forall m$.在每次迭代中,得到 $J$ 个终止结点的回归树.因此 $J$ 成为了整个 boosting 过程的 元参数(meta-parameter),根据手头上的数据来调整该参数以期最大化估计的效果.
可以考虑下式的 目标函数(target function) 的性质来得到 $J$ 的有用值
这里期望值是对 $(X,Y)$ 的总体联合分布而言.目标函数 $\eta(x)$ 是在未来数据上有最小预测风险的函数.这是我们试图近似的函数.
$\eta(X)$ 一个相关的性质是坐标变量 $X^T=(X_1,X_2,\ldots, X_p)$ 间交叉项的阶.这个可以通过它的 ANOVA 展开式得到
式子 \eqref{10.40} 中的第一项是只有一个预测变量 $X_j$ 的函数和.这些函数 $\eta_j(X_j)$ 是在所采用的误差损失准则下联合起来最能近似 $\eta(X)$ 的项.每一个 $\eta_j(X_j)$ 称为 $X_j$ 的主影响.式中第二项是那些加入到主影响中将 $\eta(X)$ 拟合得最好的含两个变量的函数.这些函数被称为每个变量对 $(X_j,X_k)$ 的二阶交叉项.式中第三项表示三阶交叉项,以此类推.对于许多实际的问题,低阶交叉影响占主要地位.如果模型得到强烈的高阶交叉影响,比如大型的决策树,则可能正确性不好.
基于树的近似的交叉性阶数被树的大小 $J$ 所限制.也就是,不存在大于 $J-1$ 阶数的交叉项.因为 \eqref{10.28} 的 boosted 模型关于树是可加的,这个限制对于它也适用.$J=2$ 时(单个分割点的“decision stump”),则只能得到仅主影响的 boosted 模型,其中不允许有交叉项.当 $J=3$ 时,可以允许有含两个变量的交叉项,以此类推.这表明选择的 $J$ 值应该反映 $\eta(x)$ 占优势的交叉项的阶数.当然这在一般情形下是未知的,但是在大部分情况下往往很低.
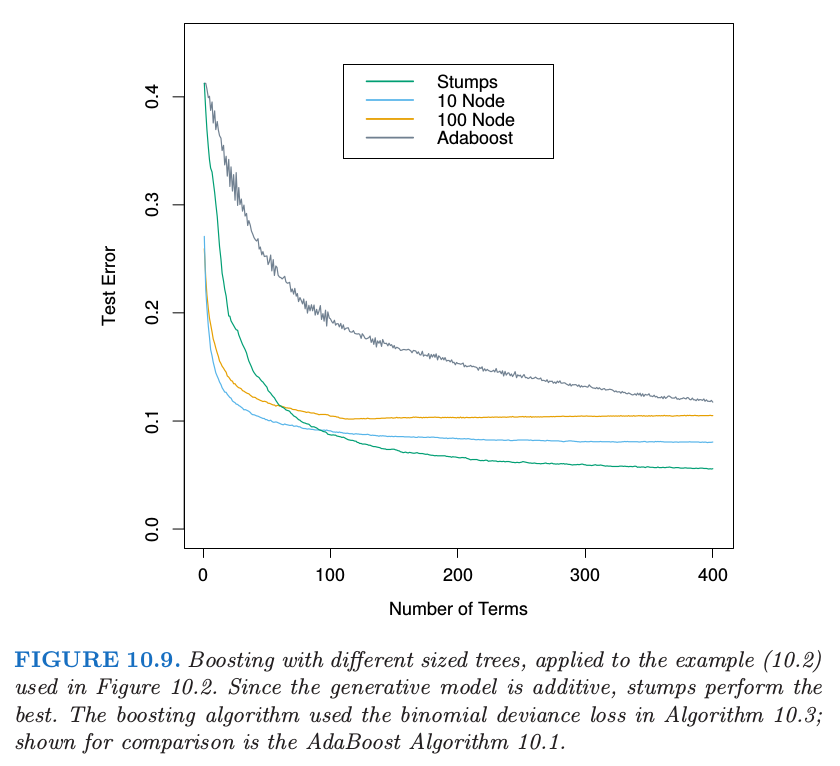
图 10.9 说明了交叉项阶数($J$ 的选择)在仿真例子 \eqref{10.2} 上的影响.
Recall
生成函数是可加的(二次单项式的和),所以 $J>2$ 的 boosting 模型产生多余的方差,也因此更高的测试误差.图 10.10 比较了用真实函数构造的 boosted stump 的坐标函数.

尽管在很多应用中,$J=2$ 是不够的,但也不太可能要求 $J>10$.经验表明 $4\le J\le 8$ 在 boosting 的情况下会取得很好的效果,这个范围内的具体取值对结果的影响并不敏感.我们可以通过尝试不同的值,然后选择一个在验证样本上低风险的 $J$ 值.然而,使用大于 $J\simeq 6$ 并不能得到显著的改善.