对 R 内置的数据集 USArrests 演示主成分的使用方法。

数据包含 50 个州，

states = row.names(USArrests)
states
##  [1] "Alabama"        "Alaska"         "Arizona"        "Arkansas"      
##  [5] "California"     "Colorado"       "Connecticut"    "Delaware"      
##  [9] "Florida"        "Georgia"        "Hawaii"         "Idaho"         
## [13] "Illinois"       "Indiana"        "Iowa"           "Kansas"        
## [17] "Kentucky"       "Louisiana"      "Maine"          "Maryland"      
## [21] "Massachusetts"  "Michigan"       "Minnesota"      "Mississippi"   
## [25] "Missouri"       "Montana"        "Nebraska"       "Nevada"        
## [29] "New Hampshire"  "New Jersey"     "New Mexico"     "New York"      
## [33] "North Carolina" "North Dakota"   "Ohio"           "Oklahoma"      
## [37] "Oregon"         "Pennsylvania"   "Rhode Island"   "South Carolina"
## [41] "South Dakota"   "Tennessee"      "Texas"          "Utah"          
## [45] "Vermont"        "Virginia"       "Washington"     "West Virginia" 
## [49] "Wisconsin"      "Wyoming"

有四个特征

names(USArrests)
## [1] "Murder"   "Assault"  "UrbanPop" "Rape"

先计算下这四个变量的均值和方差，可以发现差异很大

apply(USArrests, 2, mean)
##   Murder  Assault UrbanPop     Rape 
##    7.788  170.760   65.540   21.232
apply(USArrests, 2, var)
##     Murder    Assault   UrbanPop       Rape 
##   18.97047 6945.16571  209.51878   87.72916

所以对数据进行 scale 是很必要的，不然大部分主成分都会被 Assault 主导。采用下面命令进行主成分，

pr.out = prcomp(USArrests, scale = TRUE)

prcomp() 默认会对数据中心化，但只有指定 scale=TRUE 才能对数据方差进行标准化（标准差为 1）。返回结果中包含以下变量

names(pr.out)
## [1] "sdev"     "rotation" "center"   "scale"    "x"

其中 center 和 scale 对应进行中心化和标准化时变量的均值和标准差。rotation 返回主成分载荷。注意到一般会有 \(\min(n-1,p)\) 个主成分。

我们不需要另外计算 scores，因为 pr.out$x 就是 scores。

利用下面命令可以画出前两个主成分图象，

biplot(pr.out, scale = 0)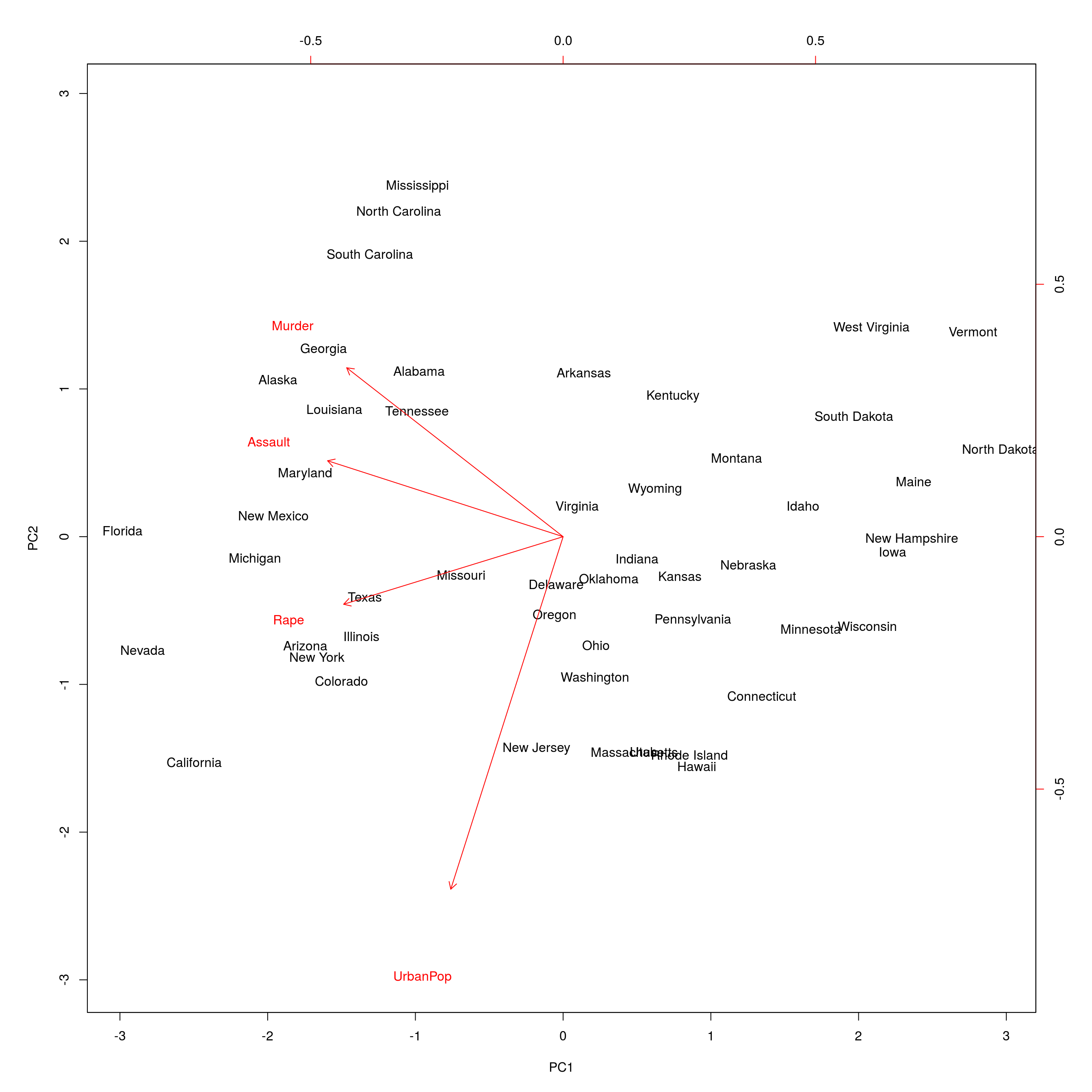

下面计算每个主成分解释的方差比例

pr.var = pr.out$sdev^2
pve = pr.var / sum(pr.var)

然后绘制 方差解释比例 (PVE) 及 累计方差解释比例 (cumulative PVE)，

plot(pve, xlab = "PC", ylab = "PVE", ylim = c(0, 1), type = 'b')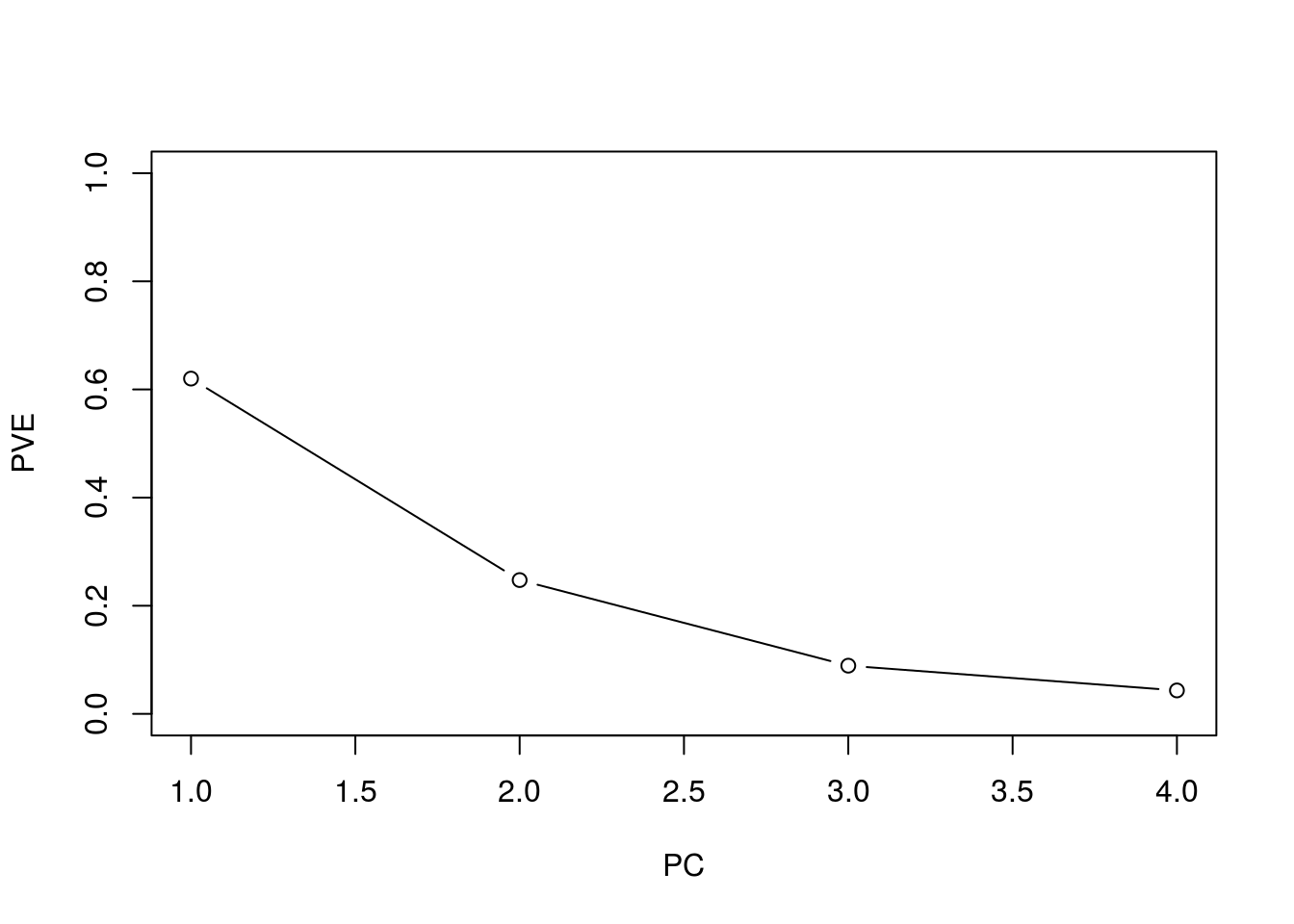

plot(cumsum(pve), xlab = "PC", ylab = "CPVE", ylim = c(0,1), type = 'b')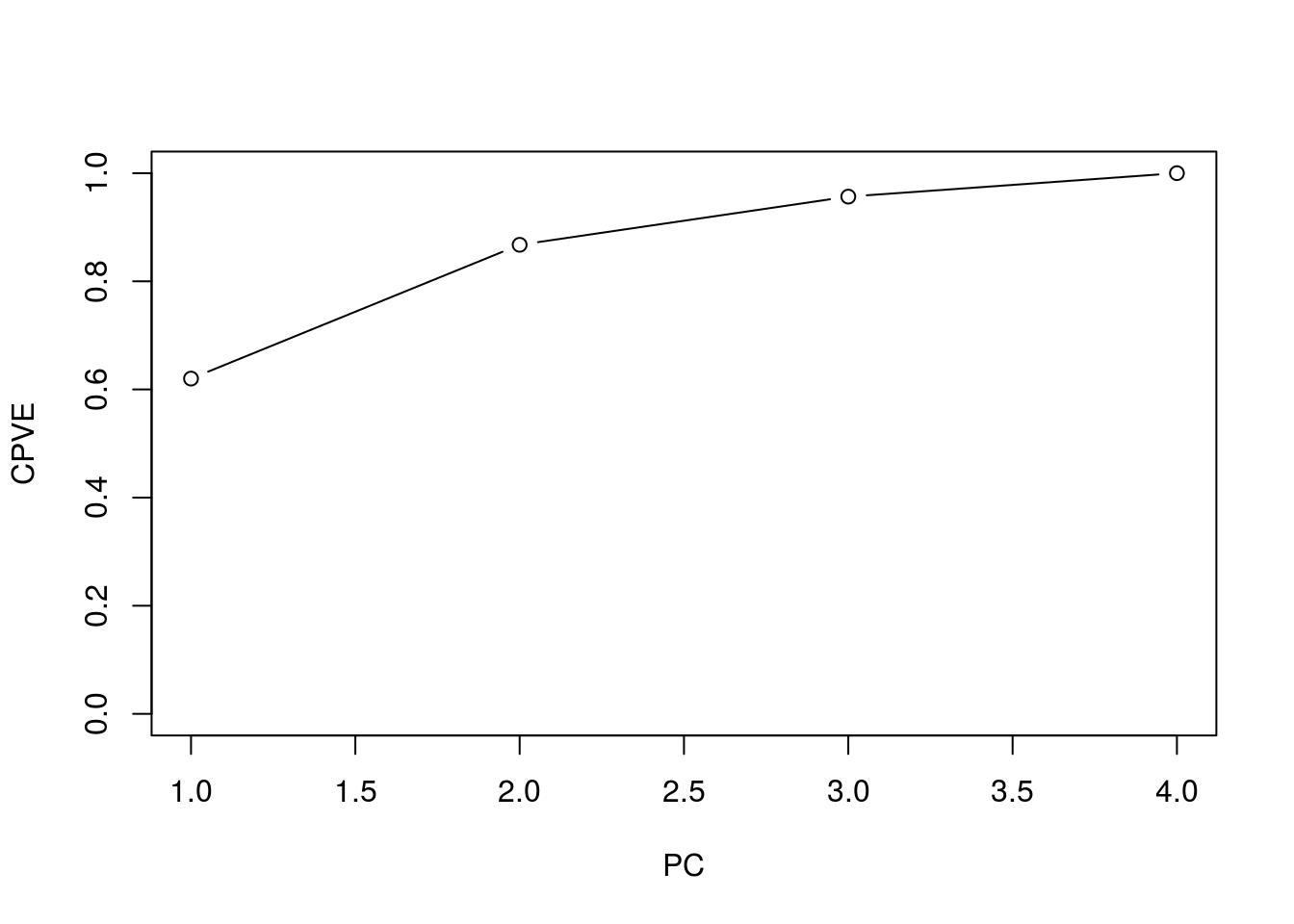

References

James, G., Witten, D., Hastie, T., & Tibshirani, R. (Eds.). (2013). An introduction to statistical learning: with applications in R. New York: Springer.

Copyright © 2016-2019 weiya